作者:JULY、二零一一年三月十八日
出處:http://blog.csdn.net/v_JULY_v
----------------------------------
引言:
來考慮一個問題,
平面上6個點,A,B,C,D,E,F,假定已知其中一些點之間的距離,
現在,要求A到其它5個點,B,C,D,E,F各點的最短距離。
如下圖所示:
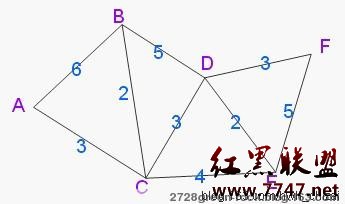
經過上圖,我們可以輕而易舉的得到A->B,C,D,E,F各點的最短距離:
目的 路徑 最短距離
A=>A, A->A 0
A=>B, A->C->B 3+2=5
A=>C, A->C 3
A=>D, A->C->D 3+3=6
A=>E, A->C->E 3+4=7
A=>F, A->C->D->F 3+3+3=9
我想,如果是單單出上述一道填空題,要你答出A->B,C,D,E,F各點的最短距離,
一個小學生,掰掰手指,也能在幾分鐘之內,填寫出來。
我們的問題,當然不是這麼簡單,上述只是一個具體化的例子而已。
實際上,很多的問題,如求圖的最短路徑問題,就要用到上述方法,不斷比較、不斷尋找,以期找到最短距離的路徑,此類問題,便是Dijkstra 算法的應用了。當然,還有BFS算法,以及更高效的A*搜尋算法。
A*搜尋算法已在本BLOG內有所詳細的介紹,本文咱們結合fibonacci堆實現Dijkstra 算法。
即,Dijkstra + fibonacci堆 c實現。
我想了下,把一個算法研究夠透徹之後,還要編寫代碼去實現它,才叫真正掌握了一個算法。本BLOG內經典算法研究系列,已經寫了18篇文章,十一個算法,所以,還有10多個算法,待我去實現。
代碼風格
實現一個算法,首先要了解此算法的原理,了解此算法的原理之後,便是寫代碼實現。
在打開編譯器之前,我先到網上搜索了一下“Dijkstra 算法+fibonacci堆實現”。
發現:網上竟沒有過 Dijkstra + fibonacci堆實現的c代碼,而且如果是以下幾類的代碼,我是直接跳過不看的:
1、沒有注釋(看不懂)。
2、沒有排版(不舒服)。
3、冗余繁雜(看著煩躁)。
fibonacci堆實現Dijkstra 算法
ok,閒話少說,咱們切入正題。下面,咱們來一步一步利用fibonacci堆實現Dijkstra 算法吧。
前面說了,要實現一個算法,首先得明確其算法原理及思想,而要理解一個算法的原理,又得知道發明此算法的目的是什麼,即,此算法是用來干什麼的?
由前面的例子,我們可以總結出:Dijkstra 算法是為了解決一個點到其它點最短距離的問題。
我們總是要找源點到各個目標點的最短距離,在尋路過程中,如果新發現了一個新的點,發現當源點到達前一個目的點路徑通過新發現的點時,路徑可以縮短,那麼我們就必須及時更新此最短距離。
ok,舉個例子:如我們最初找到一條路徑,A->B,這條路徑的最短距離為6,後來找到了C點,發現若A->C->B點路徑時,A->B的最短距離為5,小於之前找到的最短距離6,所以,便得此更新A到B的最短距離:為5,最短路徑為A->C->B.
好的,明白了此算法是干什麼的,那麼咱們先用偽代碼嘗試寫一下吧(有的人可能會說,不是吧,我現在,什麼都還沒搞懂,就要我寫代碼了。額,你手頭不是有資料麼,如果全部所有的工作,都要自己來做的話,那就是一個浩大的工程了。:D。)。
咱們先從算法導論上,找來Dijkstra 算法的偽代碼如下:
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s) //1、初始化結點工作
2 S ← Ø
3 Q ← V[G] //2、插入結點操作
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //3、從最小隊列中,抽取最小點工作
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //4、松弛操作。
偽代碼畢竟與能在機子上編譯運行的代碼,還有很多工作要做。
首先,咱們看一下上述偽代碼,可以看出,基本上,此Dijkstra 算法主要分為以下四個步驟:
1、初始化結點工作
2、插入結點操作
3、從最小隊列中,抽取最小點工作
4、松弛操作。
ok,由於第2個操作涉及到斐波那契堆,比較復雜一點,咱們先來具體分析第1、2、4個操作:
1、得用O(V)的時間,來對最短路徑的估計,和對前驅進行初始化工作。
INITIALIZE-SINGLE-SOURCE(G, s)
1 for each vertex v ∈ V[G]
2 do d[v] ← ∞
3 π[v] ← NIL //O(V)
4 d[s] 0
我們根據上述偽代碼,不難寫出以下的代碼:
void init_single_source(Graph *G,int s)
{
for (int i=0;i<G->n;i++) {
d[i]=INF;
pre[i]=-1;
}
d[s]=0;
}
2、插入結點到隊列的操作
2 S ← Ø
3 Q ← V[G] //2、插入結點操作
代碼:
for (i=0;i<G->n;i++)
S[i]=0;
4、松弛操作。
首先得理解什麼是松弛操作:
Dijkstra 算法使用了松弛技術,對每個頂點v<-V,都設置一個屬性d[v],用來描述從源點s到v的最短路徑上權值的上界,稱為最短路徑的估計。
RELAX(u, v, w)
1 if d[v] > d[u] + w(u, v)
2 then d[v] ← d[u] + w(u, v)
3 π[v] ← u //O(E)
同樣,我們不難寫出下述代碼:
void relax(int u,int v,Graph *G)
{
if (d[v]>d[u]+G->w[u][v])
{
d[v] = d[u]+G->w[u][v]; //更新此最短距離
pre[v]=u; //u為v的父結點
}
}
再解釋一下上述relax的代碼,其中u為v的父母結點,當發現其父結點d[u]加上經過路徑的距離G->w[u][v],小於子結點到源點的距離d[v],便得更新此最短距離。
請注意,說的明白點:就是本來最初A到B的路徑為A->B,現在發現,當A經過C到達B時,此路徑距離比A->B更短,當然,便得更新此A到B的最短路徑了,即是:A->C->B,C 即成為了B的父結點(如此解釋,我相信您已經明朗。:D。)。
即A=>B <== A->C->B,執行賦值操作。
ok,第1、2、4個操作步驟,咱們都已經寫代碼實現了,那麼,接下來,咱們來編寫第3個操作的代碼:3、從最小隊列中,抽取最小點工作。
相信,你已經看出來了,我們需要構造一個最小優先隊列,那用什麼來構造最小優先隊列列?對了,堆。什麼堆最好,效率最高,呵呵,就是本文要實現的fibonacci堆。
為什麼?ok,請看最小優先隊列的三種實現方法比較:
EXTRACT-MIN + RELAX
I、 簡單方式: O(V*V + E*1)
II、 二叉/項堆: O(V*lgV + |E|*lgV)
源點可達:O(E*lgV)
稀疏圖時,有E=o(V^2/lgV),