本文,即以演示圖的形式,比較它們各自的尋路過程,讓各位對它們有一個清晰而直觀的印象。
我們比較,以下五種算法:
1. A* (使用曼哈頓距離)
2. A* (采用歐氏距離)
3. A* (利用切比雪夫距離)
4. Dijkstra
5. Bi-Directional Breadth-First-Search(雙向廣度優先搜索)
咱們以下圖為例,圖上綠色方塊代表起始點,紅色方塊代表目標點,紫色的方塊代表障礙物,白色的方塊代表可以通行的路徑。
下面,咱們隨意擺放起始點綠塊,目標點紅塊的位置,然後,在它們中間隨便畫一些障礙物,
最後,運行程序,比較使用上述五種算法,得到各自不同的路徑,各自找尋過程中所覆蓋的范圍,各自的工作流程,並從中可以窺見它們的效率高低。
A*、Dijkstra、BFS算法性能比較演示:
ok,任意擺放綠塊與紅塊的三種狀態:
一、起始點綠塊,與目標點紅塊在同一條水平線上:
各自的搜尋路徑為:
1. A* (使用曼哈頓距離)
2. A* (采用歐氏距離)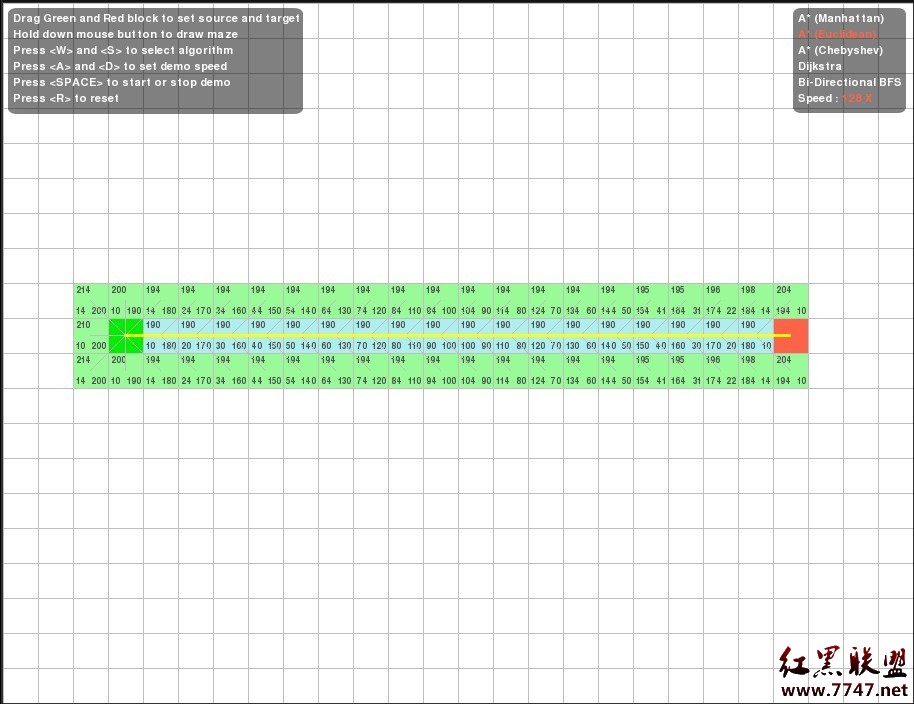
3. A* (利用切比雪夫距離)
4. Dijkstra 算法.//很明顯,Dijkstra 搜尋效率明顯差於上述A* 算法。(看它最後找到目標點紅塊所走過的路徑,和覆蓋的范圍,即能輕易看出來,下面的比較,也是基於同一個道理。看路徑,看覆蓋的范圍,評價一個算法的效率)。

5. Bi-Directional Breadth-First-Search(雙向廣度優先搜索) 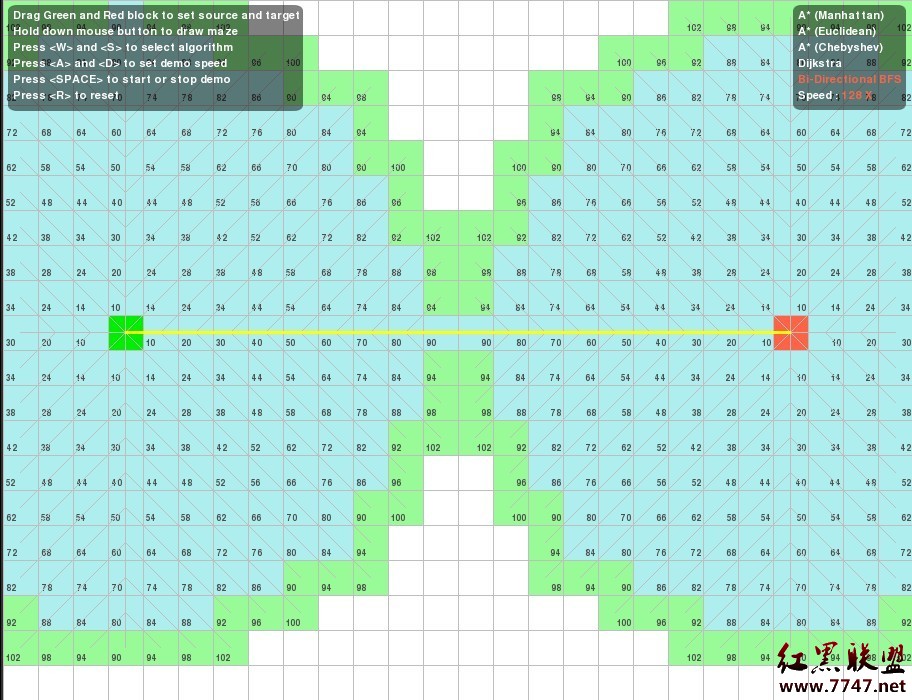
二、起始點綠塊,目標點紅塊在一斜線上:

各自的搜尋路徑為:
1. A* (使用曼哈頓距離)
2. A* (采用歐氏距離)
3. A* (利用切比雪夫距離)
4. Dijkstra 算法。 //與上述A* 算法比較,覆蓋范圍大,搜尋效率較低。

5. Bi-Directional Breadth-First-Search(雙向廣度優先搜索)
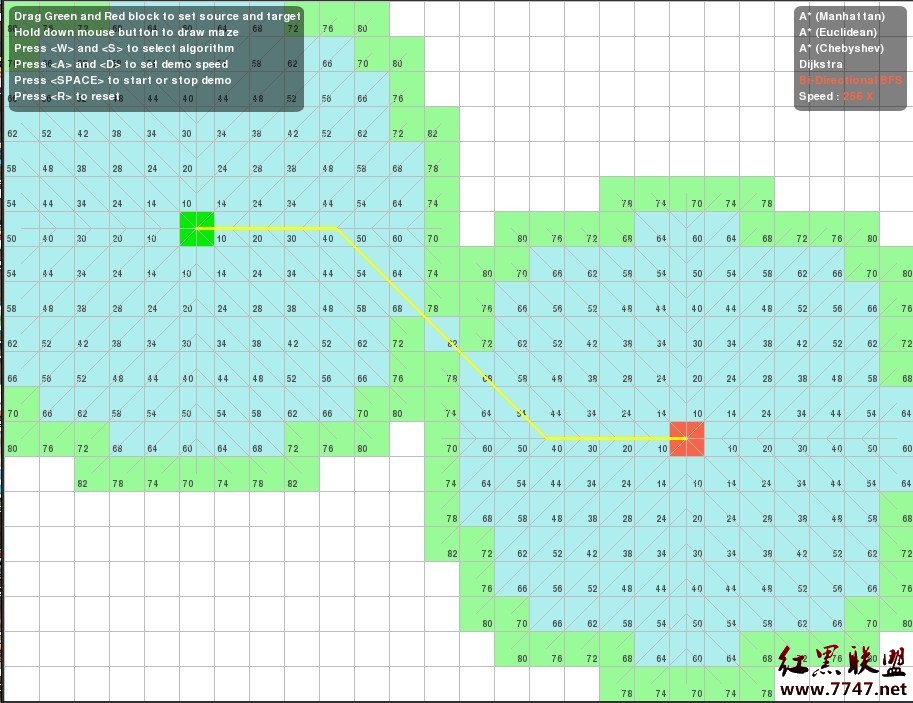
三、起始點綠塊,目標點紅塊被多重障礙物阻擋:

各自的搜尋路徑為(同樣,還是從綠塊到紅塊):
1. A* (使用曼哈頓距離)
2. A* (采用歐氏距離)..
3. A* (利用切比雪夫距離)
4. Dijkstra....
5. Bi-Directional Breadth-First-Search(雙向廣度優先搜索) //覆蓋范圍同上述Dijkstra 算法一樣很大,效率低下。

A*搜尋算法的高效之處
如上,是不是對A*、Dijkstra、雙向BFS算法各自的性能有了個總體大概的印象列?由上述演示,我們可以看出,在最短路徑搜尋效率上,一般有A*>Dijkstra、雙向BFS,其中Dijkstra、雙向BFS到底哪個算法更優,還得看具體情況。
由上,我們也可以看出,A*搜尋算法的確是一種比較高效的尋路算法。
A*算法最為核心的過程,就在每次選擇下一個當前搜索點時,是從所有已探知的但未搜索過點中(可能是不同層,亦可不在同一條支路上),選取f值最小的結點進行展