4、教你通透徹底理解:BFS和DFS優先搜索算法
作者:July 二零一一年一月一日
---------------------------------
本人參考:算法導論
本人聲明:個人原創,轉載請注明出處。
ok,開始。
翻遍網上,關於此類BFS和DFS算法的文章,很多。但,都說不出個所以然來。
讀完此文,我想,
你對圖的廣度優先搜索和深度優先搜索定會有個通通透透,徹徹底底的認識。
---------------------
咱們由BFS開始:
首先,看下算法導論一書關於 此BFS 廣度優先搜索算法的概述。
算法導論第二版,中譯本,第324頁。
廣度優先搜索(BFS)
在Prime最小生成樹算法,和Dijkstra單源最短路徑算法中,都采用了與BFS 算法類似的思想。
//u 為 v 的先輩或父母。
BFS(G, s)
1 for each vertex u ∈ V [G] - {s}
2 do color[u] ← WHITE
3 d[u] ← ∞
4 π[u] ← NIL
//除了源頂點s之外,第1-4行置每個頂點為白色,置每個頂點u的d[u]為無窮大,
//置每個頂點的父母為NIL。
5 color[s] ← GRAY
//第5行,將源頂點s置為灰色,這是因為在過程開始時,源頂點已被發現。
6 d[s] ← 0 //將d[s]初始化為0。
7 π[s] ← NIL //將源頂點的父頂點置為NIL。
8 Q ← Ø
9 ENQUEUE(Q, s) //入隊
//第8、9行,初始化隊列Q,使其僅含源頂點s。
10 while Q ≠ Ø
11 do u ← DEQUEUE(Q) //出隊
//第11行,確定隊列頭部Q頭部的灰色頂點u,並將其從Q中去掉。
12 for each v ∈ Adj[u] //for循環考察u的鄰接表中的每個頂點v
13 do if color[v] = WHITE
14 then color[v] ← GRAY //置為灰色
15 d[v] ← d[u] + 1 //距離被置為d[u]+1
16 π[v] ← u //u記為該頂點的父母
17 ENQUEUE(Q, v) //插入隊列中
18 color[u] ← BLACK //u 置為黑色
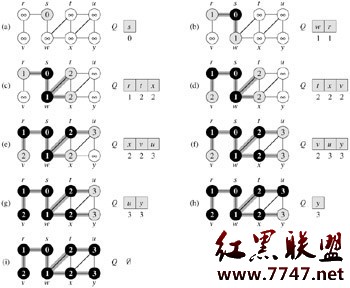
由下圖及鏈接的演示過程,清晰在目,也就不用多說了:
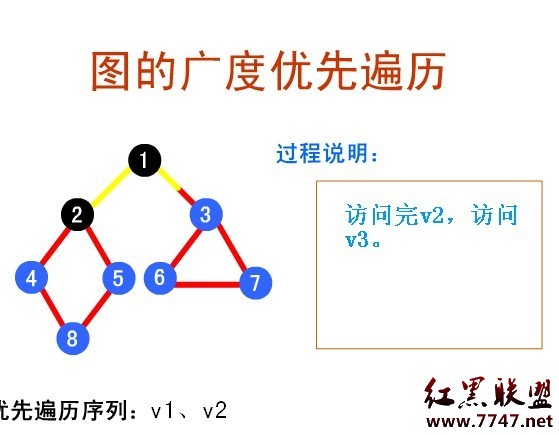
廣度優先遍歷演示地址:
html">http://sjjg.js.zwu.edu.cn/SFXX/sf1/gdyxbl.html
-----------------------------------------------------------------------------------------------------------------
ok,不再贅述。接下來,具體講解深度優先搜索算法。
深度優先探索算法 DFS
//u 為 v 的先輩或父母。
DFS(G)
1 for each vertex u ∈ V [G]
2 do color[u] ← WHITE
3 π[u] ← NIL
//第1-3行,把所有頂點置為白色,所有π 域被初始化為NIL。
4 time ← 0 //復位時間計數器
5 for each vertex u ∈ V [G]
6 do if color[u] = WHITE
7 then DFS-VISIT(u) //調用DFS-VISIT訪問u,u成為深度優先森林中一棵新的樹
//第5-7行,依次檢索V中的頂點,發現白色頂點時,調用DFS-VISIT訪問該頂點。
//每個頂點u 都對應於一個發現時刻d[u]和一個完成時刻f[u]。
DFS-VISIT(u)
1 color[u] ← GRAY //u 開始時被發現,置為白色
2 time ← time +1 //time 遞增
3 d[u] <-time //記錄u被發現的時間
4 for each v ∈ Adj[u] //檢查並訪問 u 的每一個鄰接點 v
5 do if color[v] = WHITE //如果v 為白色,則遞歸訪問v。
6 then π[v] ← u //置u為 v的先輩
7 DFS-VISIT(v) //遞歸深度,訪問鄰結點v
8 color[u] <-BLACK //u 置為黑色,表示u及其鄰接點都已訪問完成
9 f [u] ▹ time ← time +1 //訪問完成時間記錄在f[u]中。
//完
第1-3行,5-7行循環占用時間為O(V),此不包括調用DFS-VISIT的時間。
對於每個頂點v(-V,過程DFS-VISIT僅被調用依次,因為只有對白色頂點才會調用此過程。
第4-7行,執行時間為O(E)。
因此,總的執行時間為O(V+E)。
下面的鏈接,給出了深度優先搜索的演示系統:
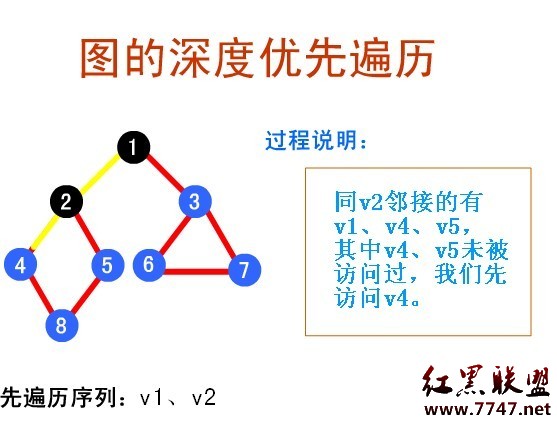
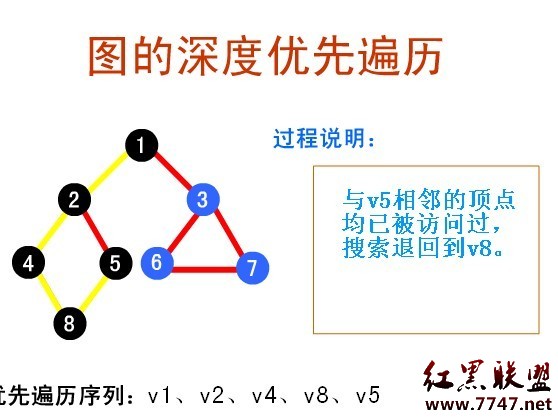
圖的深度優先遍歷演示系統:
http://sjjg.js.zwu.edu.cn/SFXX/sf1/sdyxbl.html
===============
最後,咱們再來看深度優先搜索的遞歸實現與非遞歸實現
1、DFS 遞歸實現:
void dftR(PGraphMatrix inGraph)
{
PVexType v;
assertF(inGraph!=NULL,"in dftR, pass in inGraph is null
");
printf("
===start of dft recursive version===
");
for(v=firstVertex(inGraph);v!=NULL;v=nextVertex(inGraph,v))
if(v->marked==0)
dfsR(inGraph,v);
printf("
===end of dft recursive version===
");
}
void dfsR(PGraphMatrix inGraph,PVexType inV)
{
PVexType v1;
assertF(inGraph!=NULL,"in dfsR,inGraph is null
");
assertF(inV!=NULL,"in dfsR,inV is null
");
inV->marked=1;
visit(inV);
for(v1=firstAdjacent(inGraph,inV);v1!=NULL;v1=nextAdjacent(inGraph,inV,v1))
//v1當為v的鄰接點。