作者:July 二零一一年二月十日
本文參考:
I、 維基百科、
II、 人工智能-09 啟發式搜索、
III、本BLOG內,經典算法研究系列:一、A*搜索算法
----------------------------
引言:
A*搜索算法,作為經典算法研究系列的開篇文章,之前已在本BLOG內有所闡述。
但要真正理解A*搜索算法,還是得先從啟發式搜索算法談起。
畢竟,A*搜索算法也是啟發式算法中的一種。ok,切入正題。
一、何謂啟發式搜索
啟發式搜索算法有點像廣度優先搜索,不同的是,它會優先順著有啟發性和具有特定信息的節點搜索下去
,這些節點可能是到達目標的最好路徑。
我們稱這個過程為最優(best-first)或啟發式搜索。
下面是其基本思想:
1) 假定有一個啟發式(評估)函數ˆf ,可以幫助確定下一個要擴展的最優節點,
我們采用一個約定,即ˆf的值小表示找到了好的節點。
這個函數基於指定問題域的信息,它是狀態描述的一個實數值函數。
2) 下一個要擴展的節點n是ˆf(n)值最小的節點(假定節點擴展產生一個節點的所有後
繼)。
3) 當下一個要擴展的節點是目標節點時過程終止。
我們常常可以為最優搜索指定好的評估函數。
如在8數碼問題中,可以用不正確位置的數字個數作為狀態描述好壞的一個度量:
f(n) = 位置不正確的數字個數(和目標相比)
在搜索過程中采用這個啟發式函數將產生圖9 - 1所示的圖,每個節點的數值是該節點的
值。
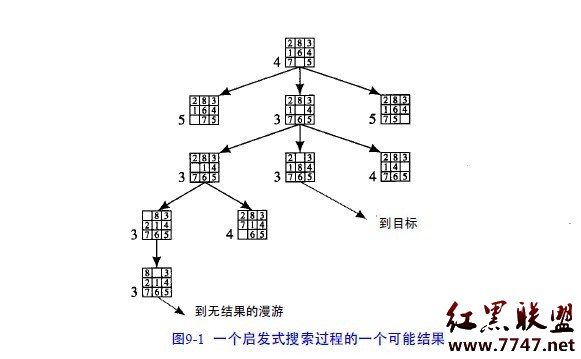
圖9-1 一個啟發式搜索過程的一個可能結果
上述例子表明,在搜索過程中我們需要偏向有利於回溯到早期路徑的搜索(為了避免由於過分的優化試探
而陷入“花園小徑”)。
因此我們加了一個“深度因子”給ˆf: ˆf(n)= gˆ(n)+ hˆ(n) ,gˆ(n)是對圖中節點n的“深度”估計(即
從開始節點到n的最短路徑長度),hˆ(n)是對節點n的啟發或評估。
像前面一樣,如果gˆ(n)= 搜索圖中節點n的深度,hˆ(n)=不正確位置的數字個數(和目標相比), 我們可以得到圖9-2。
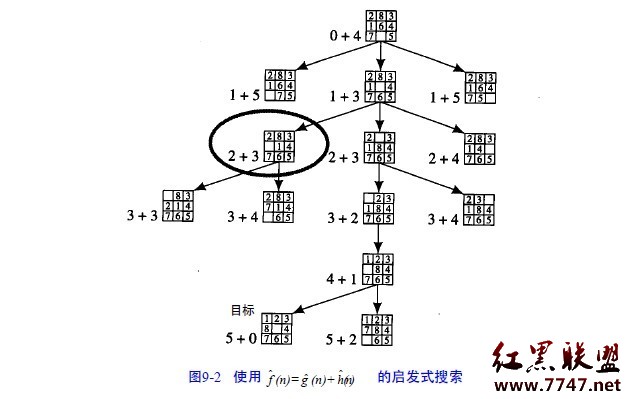
在這個圖中,把gˆ(n)和hˆ(n)的值寫在每個節點的旁邊,在這種情況下,可以看到搜索相當直接地朝著目
標進行(除了用圓圈標注的節點外)。
這些例子提出了兩個重要的問題。
第一,我們如何為最優搜索決定評估函數?
第二,最優搜索的特性是什麼?它能找到到達目標節點的好路徑嗎?
本文主要討論最優搜索的形式表示。作為例子,下面介紹一個包括最優搜索版本的一般圖搜索算法
(為了更詳細地了解啟發式搜索,可以參考引用的文章和Pearl寫的書[pearl 1984])。
二、一個通用的圖搜索算法
為了更准確地解釋啟發式搜索過程,這裡提出一個通用的圖搜索算法,它允許各種
用戶—偏愛啟發式的或盲目的,進行定制。我把這個算法叫做圖搜索(GRAPHSEARCH)。
下面是(第一個版本)它的定義。
GRAPHSEACH:
1) 生成一個僅包含開始節點n0的搜索樹Tr。把n0放在一個稱為OPEN的有序列表中。
2) 生成一個初始值為空的列表CLOSED。
3) 如果OPEN為空,則失敗並退出。
4) 選出OPEN中的第一個節點,並將它從OPEN中移出,放入CLOSED中。稱該節點為n。
5) 如果n是目標節點,順著Tr中的弧從n回溯到n0找到一條路徑,獲得解決方案,則成功退
出(弧在第6步產生)。
6) 擴展節點n,生成n的後繼節點集M。通過在Tr中建立從n到M中每個成員的弧生成n的後繼。
7) 按照任意的模式或啟發式方式對列表OPEN重新排序。
8) 返回步驟3 。
這個算法可用來執行最優搜索、廣度優先搜索或深度優先搜索。
在廣度優先搜索中,新節點只要放在OPEN的尾部即可(先進先出, FIFO),節點不用重排。
在深度優先搜索中,新節點放在OPEN的開始(後進先出,LIFO)。
在最優(也叫啟發式)搜索中,按照節點的啟發式方式來重排OPEN。
三、略談A*搜索算法
用最優搜索算法詳細說明GRAPHSEARCH。
最優搜索算法根據函數的增加值,(在上述第7步)重排OPEN中的節
點,如8數碼問題。把GRAPHSEACH的這種算法稱為算法A*。
下面將會看到,定義使A*執行廣度搜索或相同代價搜索的函數是可行的。為了確定要用的函數族,必須先
介紹一些其他符號。
設g(n) = 從開始節點n0到節點n的一個最小代價路徑的代價。
設h(n) =節點n和目標節點(遍及所有可能的目標節點以及從n到它們的所有可能路徑)之間的最小代價路徑的實際代價。
那麼f(n) = g(n) + h(n)就是從n0到目標節點並且經過節點n的最小代價路徑的代價。
注意f(n0)= h(n0)是從n0到目標節點的一個(不受限的)最小代價路徑的代價。
對每個節點n,設gˆ(n)(深度因子)是由A*發現的到節點n的最小代價路徑的代價,hˆ(n)(啟發因子)是h(n)的某個估計。
在算法A*中,我們用ˆf(n)= gˆ(n)+ hˆ(n)。
注意,如果算法A*中的恆等於0,就成為相同代價搜索。這些定義示例在圖3中。
算法A*:
1)生成一個只包含開始節點n0的搜索圖G,把n0放在一個叫OPEN的列表上。
2)生成一個列表CLOSED,它的初始值為空。
3)如果OPEN為空,則失敗退出。
4)選擇OPEN上的第一個節點,把它從OPEN中移入CLOSED,稱該節點為n。
5)如果n是目標節點,順著G中,從n到n0的指針找到一條路徑,獲得解決方案,成功退出
(該指針定義了一個搜索樹,在第7步建立)。
6)擴展節點n,生成其後繼節點集M,在G中,n的祖先不能在M中。在G中安置M的成
員,使它們成為n的後繼。
7) 從M的每一個不在G中的成員建立一個指向n的指針(例如,既不在OPEN中,也不在
CLOSED中)。把M的這些成員加到OPEN中。對的每一個已在OPEN 中或CLOSED
中的成員m,如果到目前為止找到的到達m的最好路徑通過n,就把它的指針指向n。對
已在CLOSE中的M的每一個成員,重定向它在G中的每一個後繼,以使它們順著到目前
為止發現的最好路徑指向它們的祖先。
8) 按遞增值,重排OPEN(相同最小值可根據搜索樹中的最深節點來解決)。
9) 返回第3步。
在第7步中,如果搜索過程發現一條路徑到達一個節點的代價比現存的路徑代價低,
我們就要重定向指向該節點的指針。已經在CLOSED中的節點子孫的重定向保存了後面
的搜索結果,但是可能需要指數級的計算代價。因此,第7步常常不會實現。隨著搜索
的向前推進,其中有些指針最終將會被重定向。
更多,可參考:html" target=_blank>經典算法研究系列:一、A*搜索算法: 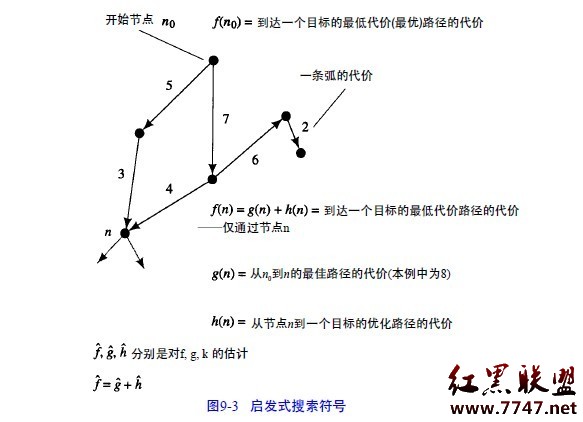
四、啟發式算法相關問題
4.1、啟發式算法與最短路徑問題
啟發式通常用於資訊充份的搜尋算法,例如最好優先貪婪算
法與A*。
最好優先貪婪算法會為啟發式函數選擇最低代價的節點;
A*則會為g(n) + h(n)選擇最低代價的節點,此g(n)是從起始節點到目前節點的路徑的確實代價。
如果h(n)是可接受的(admissible)意即h(n)未曾付出超過達到目標的代價,則A*一定會找出最佳解。
最能感受到啟發式算法好處的經典問題是n-puzzle。此問題在計算錯誤的拼圖圖形,與計算任兩塊拼圖的曼哈頓距離的總和以及它距離目的有多遠時,使用了本算法。注意,上述兩條件都必須在可接受的范圍內。
曼哈頓距離是一個簡單版本的n-puzzle問題,因為我們假設可以獨立移動一個方塊到我們想要的位置,而暫不考慮會移到其他方塊的問題。
給我們一群合理的啟發式函式h1(n),h2(n),...,hi(n),而函式h(n) = max{h1(n),h2(n),...,hi(n)}則是
個可預測這些函式的啟發式函式。
一個在1993年由A.E. Prieditis寫出的程式ABSOLVER就運用了這些技術,這程式可以自動為問題產生啟發
式算法。ABSOLVER為8-puzzle產生的啟發式算法優於任何先前存在的!而且它也發現了第一個有用的解魔
術方塊的啟發式程式。
4.2、啟發式算法對運算效能的影響
任何的搜尋問題中,每個節點都有b個選擇以及到達目標的深度d,一個毫無技巧的算法通常都要搜尋bd個
節點才能找到答案。
啟發式算法借由使用某種切割機制降低了分叉率(branching factor)以改進搜尋效率,由b降到較低的b。分叉率可以用來定義啟發式算法的偏序關系,例如:若在一個n節點的搜尋樹上,
h1(n)的分叉率較h2(n)低,則 h1(n) < h2(n)。
啟發式為每個要解決特定問題的搜尋樹的每個節點提供了較低的分叉率,因此它們擁有較佳效率的計算能力。
完。