作者:July、二零一一年三月十二日
出處:http://blog.csdn.net/v_JULY_v
參考:Rob Hess維護的sift 庫
環境:windows xp+vc6.0
條件:c語言實現。
說明:本BLOG內會陸續一一實現所有經典算法。
------------------------
引言:
在我寫的關於sift算法的前倆篇文章裡頭,已經對sift算法有了初步的介紹:九、圖像特征提取與匹配之SIFT算法,而後在:九(續)、sift算法的編譯與實現裡,我也簡單記錄下了如何利用opencv,gsl等庫編譯運行sift程序。
但據一朋友表示,是否能用c語言實現sift算法,同時,盡量不用到opencv,gsl等第三方庫之類的東西。而且,Rob Hess維護的sift 庫,也不好懂,有的人根本搞不懂是怎麼一回事。
那麼本文,就教你如何利用c語言一步一步實現sift算法,同時,你也就能真正明白sift算法到底是怎麼一回事了。
ok,先看一下,本程序最終運行的效果圖,sift 算法分為五個步驟(下文詳述),對應以下第二--第六幅圖:
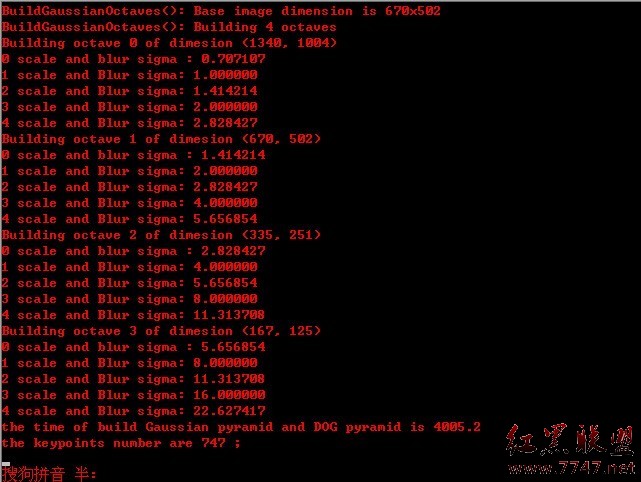



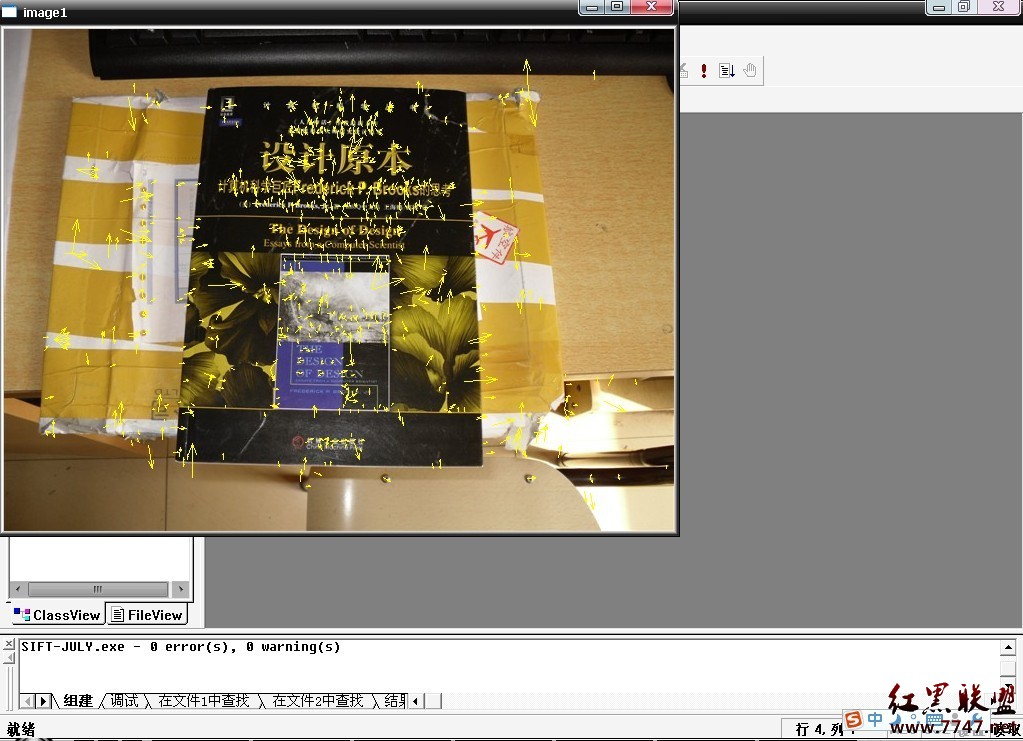
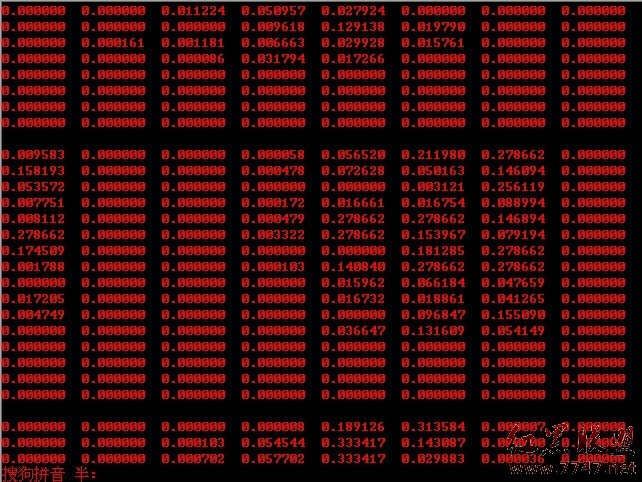
sift算法的步驟
要實現一個算法,首先要完全理解這個算法的原理或思想。咱們先來簡單了解下,什麼叫sift算法:
sift,尺度不變特征轉換,是一種電腦視覺的算法用來偵測與描述影像中的局部性特征,它在空間尺度中尋找極值點,並提取出其位置、尺度、旋轉不變量,此算法由 David Lowe 在1999年所發表,2004年完善總結。
所謂,Sift算法就是用不同尺度(標准差)的高斯函數對圖像進行平滑,然後比較平滑後圖像的差別,
差別大的像素就是特征明顯的點。
以下是sift算法的五個步驟:
一、建立圖像尺度空間(或高斯金字塔),並檢測極值點
首先建立尺度空間,要使得圖像具有尺度空間不變形,就要建立尺度空間,sift算法采用了高斯函數來建立尺度空間,高斯函數公式為:
G(x,y,e) = [1/2*pi*e^2] * exp[ -(x^2 + y^2)/2e^2]
上述公式G(x,y,e),即為尺度可變高斯函數。
而,一個圖像的尺度空間L(x,y,e) ,定義為原始圖像I(x,y)與上述的一個可變尺度的2維高斯函數G(x,y,e) 卷積運算。
即,原始影像I(x,y)在不同的尺度e下,與高斯函數G(x,y,e)進行卷積,得到L(x,y,e),如下:
L(x,y,e) = G(x,y,e)*I(x,y)
以上的(x,y)是空間坐標, e,是尺度坐標,或尺度空間因子,e的大小決定平滑程度,大尺度對應圖像的概貌特征,小尺度對應圖像的細節特征。大的e值對應粗糙尺度(低分辨率),反之,對應精細尺度(高分辨率)。
尺度,受e這個參數控制的表示。而不同的L(x,y,e)就構成了尺度空間,具體計算的時候,即使連續的高斯函數,都被離散為(一般為奇數大小)(2*k+1) *(2*k+1)矩陣,來和數字圖像進行卷積運算。
隨著e的變化,建立起不同的尺度空間,或稱之為建立起圖像的高斯金字塔。
但,像上述L(x,y,e) = G(x,y,e)*I(x,y)的操作,在進行高斯卷積時,整個圖像就要遍歷所有的像素進行卷積(邊界點除外),於此,就造成了時間和空間上的很大浪費。
為了更有效的在尺度空間檢測到穩定的關鍵點,也為了縮小時間和空間復雜度,對上述的操作作了一個改建:即,提出了高斯差分尺度空間(DOG scale-space)。利用不同尺度的高斯差分與原始圖像I(x,y)相乘 ,卷積生成。
D(x,y,e) = ((G(x,y,ke) - G(x,y,e)) * I(x,y)
= L(x,y,ke) - L(x,y,e)
DOG算子計算簡單,是尺度歸一化的LOG算子的近似。
ok,耐心點,咱們再來總結一下上述內容:
1、高斯卷積
在組建一組尺度空間後,再組建下一組尺度空間,對上一組尺度空間的最後一幅圖像進行二分之一采樣,得到下一組尺度空間的第一幅圖像,然後進行像建立第一組尺度空間那樣的操作,得到第二組尺度空間,公式定義為
L(x,y,e) = G(x,y,e)*I(x,y)
圖像金字塔的構建:圖像金字塔共O組,每組有S層,下一組的圖像由上一組圖像降采樣得到,效果圖,圖A如下(左為上一組,右為下一組):
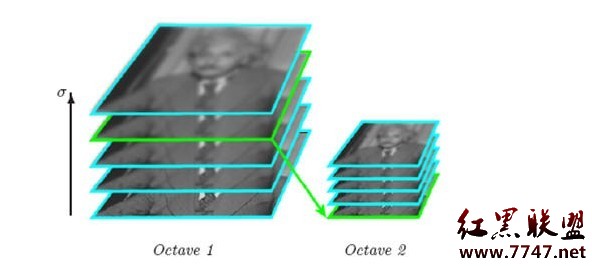
2、高斯差分
在尺度空間建立完畢後,為了能夠找到穩定的關鍵點,采用高斯差分的方法來檢測那些在局部位置的極值點,即采用倆個相鄰的尺度中的圖像相減,即公式定義為:
D(x,y,e) = ((G(x,y,ke) - G(x,y,e)) * I(x,y)
= L(x,y,ke) - L(x,y,e)
效果圖,圖B:
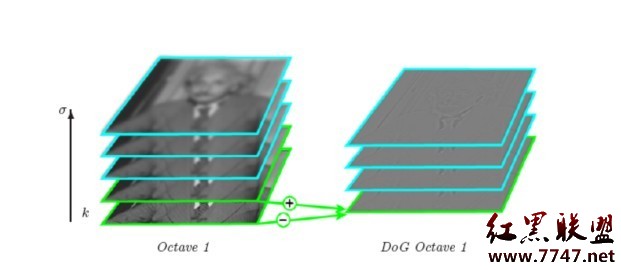
SIFT的精妙之處在於采用圖像金字塔的方法解決這一問題,我們可以把兩幅圖像想象成是連續的,分別以它們作為底面作四稜錐,就像金字塔,那麼每一個 截面與原圖像相似,那麼兩個金字塔中必然會有包含大小一致的物體的無窮個截面,但應用只能是離散的,所以我們只能構造有限層,層數越多當然越好,但處理時 間會相應增加,層數太少不行,因為向下采樣的截面中可能找不到尺寸大小一致的兩個物體的圖像。
咱們再來具體闡述下構造D(x,y,e)的詳細步驟:
1、首先采用不同尺度因子的高斯核對圖像進行卷積以得到圖像的不同尺度空間,將這一組圖像作為金子塔圖像的第一層。
2、接著對第一層圖像中的2倍尺度圖像(相對於該層第一幅圖像的2倍尺度)以2倍像素距離進行下采樣來得到金子塔圖像的第二層中的第一幅圖像,對該圖像采用不同尺度因子的高斯核進行卷積,以獲得金字塔圖像中第二層的一組圖像。
3、再以金字塔圖像中第二層中的2倍尺度圖像(相對於該層第一幅圖像的2倍尺度)以2倍像素距離進行下采樣來得到金字塔圖像的第三層中的第一幅圖像,對該圖像采用不同尺度因子的高斯核進行卷積,以獲得金字塔圖像中第三層的一組圖像。這樣依次類推,從而獲得了金字塔圖像的每一層中的一組圖像,如下圖所示:

4、對上圖得到的每一層相鄰的高斯圖像相減,就得到了高斯差分圖像,如下述第一幅圖所示。下述第二幅圖中的右列顯示了將每組中相鄰圖像相減所生成的高斯差分圖像的結果,限於篇幅,圖中只給出了第一層和第二層高斯差分圖像的計算(下述倆幅圖統稱為圖2):

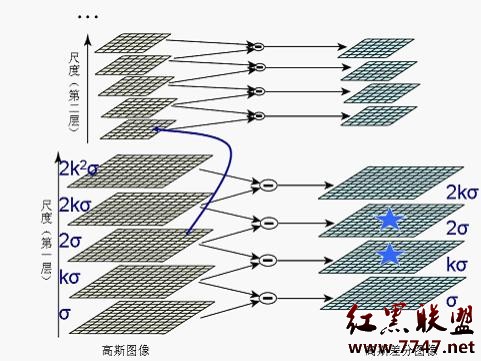
5、因為高斯差分函數是歸一化的高斯拉普拉斯函數的近似,所以可以從高斯差分金字塔分層結構提取出圖像中的極值點作為候選的特征點。對DOG 尺度空間每個點與相鄰尺度和相鄰位置的點逐個進行比較,得到的局部極值位置即為特征點所處的位置和對應的尺度。
二、檢測關鍵點
為了尋找尺度空間的極值點,每一個采樣點要和它所有的相鄰點比較,看其是否比它的圖像域和尺度域的相鄰點大或者小。如下圖,圖3所示,中間的檢測點和它同尺度的8個相鄰點和上下相鄰尺度對應的9×2個點共2