作者：July、dznlong   二零一一年二月二十二日

推薦閱讀：The Scientist and Engineers Guide to Digital Signal Processing<，By Steven W. Smith, Ph.D。此書地址：http://www.dspguide.com/pdfbook.htm。
------------
從頭到尾徹底理解傅裡葉變換算法、上
前言
第一部分、  DFT
第一章、傅立葉變換的由來
第二章、實數形式離散傅立葉變換（Real DFT）

從頭到尾徹底理解傅裡葉變換算法、下
第三章、復數
第四章、復數形式離散傅立葉變換

   前期回顧，在上一篇：html" target=_blank>十、從頭到尾徹底理解傅裡葉變換算法、上裡，我們講了傅立葉變換的由來、和實數形式離散傅立葉變換（Real DFT）倆個問題，
本文接上文，著重講下復數、和復數形式離散傅立葉變換等倆個問題。

第三章、復數

        復數擴展了我們一般所能理解的數的概念，復數包含了實數和虛數兩部分，利用復數的形式可以把由兩個變量表示的表達式變成由一個變量(復變量)來表達，使得處理起來更加自然和方便。
        我們知道傅立葉變換的結果是由兩部分組成的，使用復數形式可以縮短變換表達式，使得我們可以單獨處理一個變量（這個在後面的描述中我們就可以更加確切地知道），而且快速傅立葉變換正是基於復數形式的，所以幾乎所有描述的傅立葉變換形式都是復數的形式。
       但是復數的概念超過了我們日常生活中所能理解的概念，要理解復數是較難的，所以我們在理解復數傅立葉變換之前，先來專門復習一下有關復數的知識，這對後面的理解非常重要。
 
一、 復數的提出
 
      在此，先讓我們看一個物理實驗：把一個球從某點向上拋出，然後根據初速度和時間來計算球所在高度，這個方法可以根據下面的式子計算得出：

其中h表示高度，g表示重力加速度(9.8m/s2)，v表示初速度，t表示時間。現在反過來，假如知道了高度，要求計算到這個高度所需要的時間，這時我們又可以通過下式來計算：

              
      經過計算我們可以知道，當高度是3米時，有兩個時間點到達該高度：球向上運動時的時間是0.38秒，球向下運動時的時間是1.62秒。但是如果高度等於10時，結果又是什麼呢？根據上面的式子可以發現存在對負數進行開平方運算，我們知道這肯定是不現實的。
      第一次使用這個不一般的式子的人是意大利數學家Girolamo Cardano（1501-1576），兩個世紀後，德國偉大數學家Carl Friedrich Gause（1777-1855）提出了復數的概念，為後來的應用鋪平了道路，他對復數進行這樣表示：復數由實數（real）和虛數(imaginary)兩部分組成，虛數中的根號負1用i來表示（在這裡我們用j來表示，因為i在電力學中表示電流的意思）。
 
       我們可以把橫坐標表示成實數，縱坐標表示成虛數，則坐標中的每個點的向量就可以用復數來表示，如下圖：
               
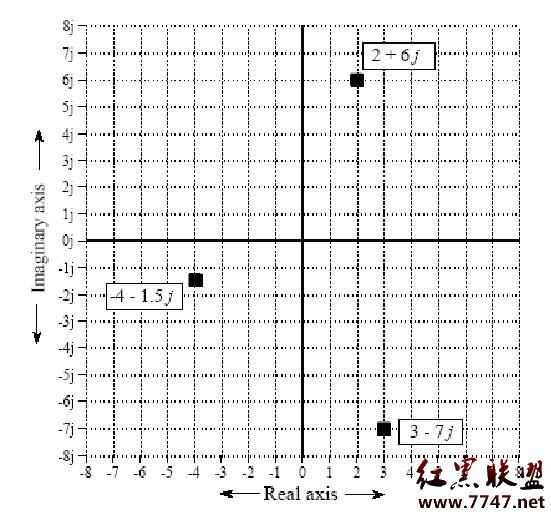
       上圖中的ABC三個向量可以表示成如下的式子：
 
            A = 2 + 6j
            B = -4 – 1.5j
            C = 3 – 7j
 
       這樣子來表達方便之處在於運用一個符號就能把兩個原來難以聯系起來的數組合起來了，不方便的是我們要分辨哪個是實數和哪個是虛數，我們一般是用Re( )和Im( )來表示實數和虛數兩部分，如：
 
            Re A = 2      Im A = 6
            Re B = -4     Im B = -1.5
            Re C = 3      Im C = -7 
 
       復數之間也可以進行加減乘除運算：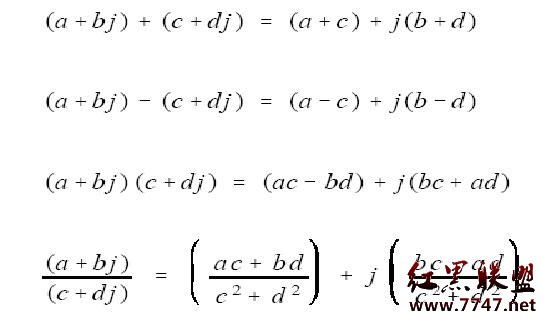
            
  
       這裡有個特殊的地方是j2等於-1，上面第四個式子的計算方法是把分子和分母同時乘以c – dj，這樣就可消去分母中的j了。
 
       復數也符合代數運算中的交換律、結合律、分配律：
 
              A B = B A
              (A + B) + C = A + (B + C)
              A(B + C) = AB + AC
 
 
二、 復數的極坐標表示形式
 
       前面提到的是運用直角坐標來表示復數，其實更為普遍應用的是極坐標的表示方法，如下圖：

              
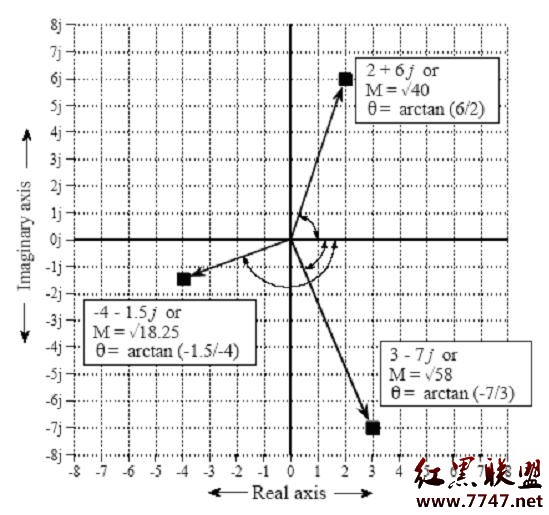
       上圖中的M即是數量積(magnitude)，表示從原點到坐標點的距離，θ是相位角(phase angle)，表示從X軸正方向到某個向量的夾角，下面四個式子是計算方法：
                     
     我們還可以通過下面的式子進行極坐標到直角坐標的轉換：
 
             a + jb = M (cosθ + j sinθ)

     上面這個等式中左邊是直角坐標表達式，右邊是極坐標表達式。
 
     還有一個更為重要的等式——歐拉等式（歐拉，瑞士的著名數學家，Leonhard Euler，1707-1783）：
             ejx = cos x + j sin x 
 
     這個等式可以從下面的級數變換中得到證明：

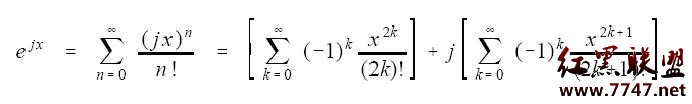
      上面中右邊的兩個式子分別是cos(x)和sin(x)的泰勒(Taylor)級數。
 

      這樣子我們又可以把復數的表達式表示成指數的形式了：
 
             a + jb = M ejθ （這便是復數的兩個表達式）
 
      指數形式是數字信號處理中數學方法的支柱，也許是因為用指數形式進行復數的乘除運算極為簡單的緣故吧：

             
三、復數是數學分析中的一個工具
 
       為什麼要使用復數呢？其實它只是個工具而已，就如釘子和錘子的關系，復數就象那錘子，作為一種使用的工具。我們把要解決的問題表達成復數的形式（因為有些問題用復數的形式進行運算更加方便），然後對復數進行運算，最後再轉換回來得到我們所需要的結果。
 
       有兩種方法使用復數，一種是用復數進行簡單的替換，如前面所說的向量表達式方法和前一節中我們所討論的實域DFT，另一