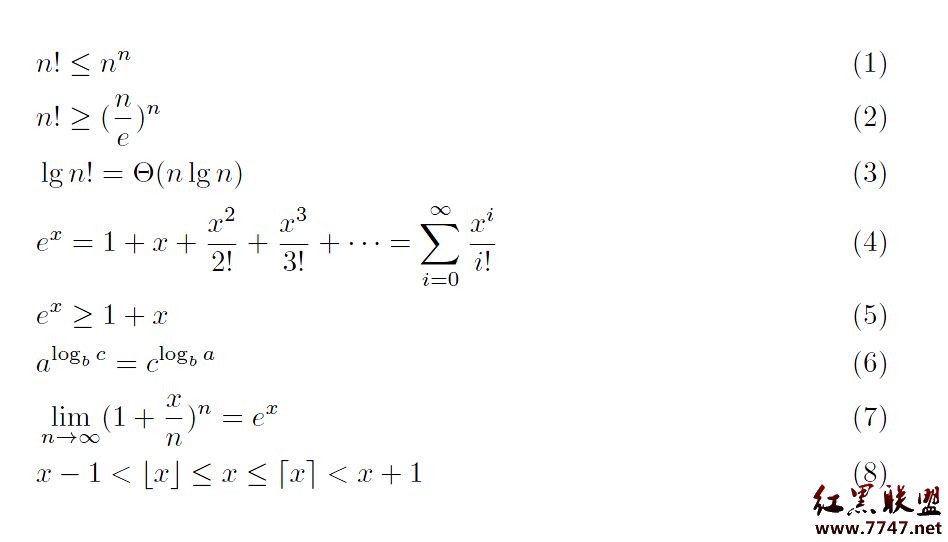劉子韬
說到算法,大家最熟悉的恐怕就是這個大歐標記了,即O。什麼基於比較的排序算法最好是O(nlgn)了什麼的。(注,本系列文章裡不區分log和lg,兩個符號都是表示以二為底的對數)
更general一點,我們可以寫成O(g(n)),這個東西是什麼嗎,其實他是一個集合,表示所以滿足條件的一系列函數,這一系列函數有什麼特點呢?那就是g(n)是他們的上界,更准確的說,是一個constant c, c*g(n)是他們的上界。如下圖,(截自算法導論)
假設f(n)表示我們quick sort的時間,我們寫作f(n) = O(nlgn),這時候你可能要問了,剛才上面不是說O(nlgn)表示一個集合嗎,這麼集合裡面顯然都是函數,那怎麼能寫 函數 = 函數的集合呢?沒錯,其實這樣寫確實不好,但是我們現在已經約定俗成了,這裡的等號就表示元素和集合關系的屬於的符號。
現在來看一下Big O的formal的定義。
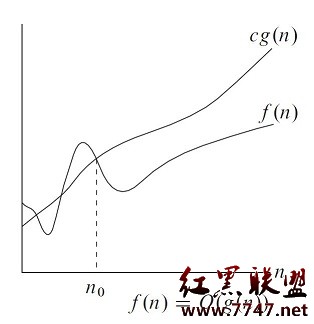
O(g(n)) = {f(n) : 存在一個正常數c,和一個 N0, 對於所有的N>N0, 0<= f(n) <= c*g(n)}
其實結合上面的圖和這個定義,Big O的意思還是很明顯的。他是f(n)的一個upper bound。
同理,我們可以定義 Big Omega 和 Theta。
Omega(g(n)) = {f(n): 存在一個正常數c,和一個 N0, 對於所有的N>N0, 0<= c*g(n) <= f(n) }
當然,這是我們f(n)的一個lower bound。
Theta(g(n)) = {f(n): 存在正常數c1和c2,和一個 N0, 對於所有的N>N0, c1*g(n) <= f(n) <= c2*g(n)}
下面是算法導論裡面完整的圖。
下面給一下Litter O 和 Litter Omega的概念。
通過上面的定義我們可以發現,在Big O,Big Omega和Theta的定義中,我們都出現了“=”,當然,類比當我們數字的比較,我們有大於等於,小於等於,同樣,我們也有大於,小於。
當然對於這個等號,我們可以說是一個tight的bound,比如2n^2 = O(n^2),這個bound就是asymptotically tight的,但是對於2n = O(n^2)來說,這個就不是tight的。所以,這時我們的Little O就孕育而生了。用算法導論裡面的原話就是: We use o-notation(Litter O) to denote an upper bound that is not asymptotically tight.
下面來看Little O的formal的定義。
o(g(n)) = {f(n): 對於任意的正常數c,存在一個N0,對於所有的N>N0, 0<= f(n) < c*g(n)}
同樣,我們可以定義Little Omega。
w(g(n)) = {f(n): 對於任意的正常數c,存在一個N0,對於所有的N>N0, 0<= c*g(n) <=f(n)}
============================================華麗的分割線==================================
對於這些標記,其實我們還可以從growth rate和極限的方面來考慮。
比如對於little O, it means that g(x) grows much faster than f(x), or similarly, the growth off(x) is nothing compared to that of g(x).(偷懶一下,直接從wikipedia上抄下來)
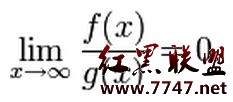
其余的大家自己也應該都可以琢磨出來。(*^__^*) 嘻嘻……
最後給幾個常用且簡單的數學公式,權當remind了。