劉子韬
動態規劃,Dynamic Programming。這裡的programming沒有翻譯成編程,是因為,這裡的programming的意思是指一個tabular method。其實這也暗示了DP的本質,用一個table保存子問題的中間結果。(後面會有例子具體介紹)
和分治算法比較類似,但不同的是分治算法把原問題劃歸為幾個相互獨立的子問題,從而一一解決,而動態規劃則是針對子問題有重疊的情況的一種解決方案。
目前design DP主要有兩個思路:
一個是利用recursive method,即首先把問題用遞歸的方法解決,然後用一個table保存recursive中的中間結果,這不就避免了遞歸中重復計算的低效了嗎?遇到需要計算以前計算過的東西,直接查表就OK,總之一句話,先寫recursive,然後比葫蘆畫瓢基本就能把DP的方法寫出來。這裡的難點是如何找到recursive。算法導論裡面也給的是這個思路。下面的前三個例子全部出自《算法導論》。
另一個思路是exhaust search,這個好像是我們老師發明的方法,這裡有篇Kirk的論文, How to design dynamic programming algorithms sans recursion 有興趣的大家可以仔細研究一下,我下面也會簡單舉例介紹一下這個方法。
下面的例子中多數代碼都是偽代碼,旨在illustrate idea。同時節省時間。代碼中都省去了backtrack的過程,即只得到了optimal solution的值,省去了如何construct optimal solution的過程。這個一般用一個數組記錄一下就OK了。
先來個比較簡單的例子(其實後面的也不難O(∩_∩)O~)
例:Rod-cutting problem(切木頭問題。感覺翻譯過來怎麼就變了味呢?囧。。。)
Input:有一個長n米的木頭,和一個price table,table如下:
長度 i 1 2 3 4 5 6 。。。
價格 Pi 1 5 8 9 10 17。。。
意思很明顯,就是長度為1米的木頭可以買1元,長5米的可以賣10元,依次類推
Output:找一個cut的方法,使最後賺的錢最多。
很顯然,這個遞歸的主要思路是我切一刀之後,分成兩段,一段我按table的價錢賣了,另一段我當成一個新的子問題,繼續作為我的函數的新的參數,這樣不就遞歸了嗎?(*^__^*) 但是問題是這一刀怎麼切,沒錯,我們就來個找最大值,即max_{i =1 to n} Pi + Cut(n-i).
所以,遞歸函數應該是:
Cut(P, n){ //P 就是我的table,n是木頭長度
if n == 0
return 0;
q = -infinity
for i = 1 to n
q = max(q,P[i]+Cut(P,n-i))
return q;
}
然後,根據這個recursive寫DP
Cut(P, n){
for(int i = 1; i<=n; i++){
q = -infinity;
for(int j = 1; j<=i; j++)
q = max(q, P[j] + r[i-j]);
r[i] = q;
}
return r[n];
}
例 最長公共字串 Longest common subsequence problem
問題描述:這個,很。。。顯而易見吧,不知道的,。。。看這裡 http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
當然這裡,我們也是要先找遞歸的。假設我的兩個sequence,一個是X,長度為n;另一個是Y,長度為m。
現在假設我有兩個point,一個是i,指在X的最後一個元素上,另一個是j,指在Y的最後一個元素上。我們的遞歸應該是分三種情況的。
1)如果X[i] == Y[j] 那麼LCS(X[i],Y[j]) = LCS(X[i-1],Y[j-1]) + 1
這個很明顯,因為發現了一組公共元素,就看剩下的有多少公共元素。
2) 如果X[i] != Y[j] 那麼 LCS(X[i],Y[j]) = max( LCS(X[i-1], Y[j]), LCS(X[i], Y[j-1]) )
這個其實也很容易相同,就是如果發現不同的,就去掉X或Y的最後一個,然後和另一個完整的比較,這樣去掉X還是Y的最後一個,就有兩種可能,所以就是要找中間max的一個。
3) 如果 i=0 或者 j=0,就return 0
因為有一個sequence已經完了。
所以遞歸這裡還是比較明顯的:
LCS(n,m){
if m==0 || n==0
return 0;
if(X[n] == Y[m])
return LCS(n-1,m-1)+1;
else
return max( LCS(n,m-1), LCS(n-1,m) );
}
現在有了遞歸,我們就應該能把它寫成tabular的DP。
初始化:Table LCS的第一行第一列都設為0。
for i = 1 to m
for j = 1 to n
if(X[i]==Y[j])
LCS[i,j] = LCS[i-1,j-1]+1;
else
LCS[i,j] = max(LCS[i,j-1], LCS[i-1,j] );
例 矩陣鏈相乘,求最小的乘法次數的問題
問題具體描述,看這裡 http://en.wikipedia.org/wiki/Matrix_chain_multiplication
先形式化一下我們的input,矩陣鏈{A1,A2,...,An},其中對於矩陣Ai,它是一個Pi-1 * Pi的矩陣。m[i,j] 表示{Ai,Ai+1,..., Aj}相乘的最小的乘法次數(強烈呼吁出現一個類似Latex功能的插件)
這個遞歸的思路其實和第一個問題有點類似,先看怎麼遞歸。
首先我們要找出一個點來分隔這個鏈,相當於這個點把這個問題轉換為了 該點前一部分的矩陣鏈的最小的乘法次數問題和該點後一部分的矩陣鏈的最小的乘法次數問題。
但是這個點怎麼找呢?和第一個例子一樣,我們直接遍歷的來找。
所以我們的遞歸應該是這樣的:
m[i,j] = min_{i<= k <=j} (m[i,k] + m[k+1,j] + Pi-1*Pk*Pj)
當然,這是對於i!=j的情況,當i==j的時候呢?顯然 是0了,因為我們的矩陣鏈就一個矩陣。
即
Matrix-chain(i,j){
if(i==j)
return 0;
q = infinity;
for k = i to j
q = min(q, Matrix-chain(i,k)+Matrix-chain(k+1,j)+Pi-1*Pk*Pj );
return q;
}
現在就是把這個recursive的東西搞成DP了。算法導論上有具體的代碼,這裡只寫個簡要的。
之類就假設我們保存中間結果的是一個n*n的table m.
初始化:m的對角元素初始化為0.
for l = 2 to n
for i=1 to n-l+1
j = i+l-1
m[i,j] = infinity
for k=i to j-1
q = m[i,k]+m[k+1,j]+Pi-1*Pk*Pj;
if(q < m[i,j])
m[i,j] = q;
return m
參照上面的recursive的例子,這個DP的代碼應該不難理解。
例 最長回文序列
回文序列就是從左往右讀和從右往左讀是一樣的。比如civic,racecar, and aibohphobia。其中長度為1的所有string都是回文的。
目標就是給一個string,找出這個string中最長的回文序列,比如給character,找出carac。
下面主要介紹一下,我們老師發明的那個方法,窮盡搜索加減枝~還是exhaust search with pruning好聽 O(∩_∩)O~
這個方法的主要思想也就是首先通過構造一棵樹,使得樹的葉子節點成為一個可能的最終的解,換句話說也就是最後的答案一定蘊育在樹的最下面一層的某個葉子節點中。很顯然,一般情況下這個樹還是比較好構造的,畢竟不用考慮什麼條件,就是一個exhaust 展開的過程,但是隨著這個樹的展開,分枝越來越多,這樣肯定是不make sense的,所以需要找到一些pruning rules,來修剪這棵樹。其實說了半天,肯定也比較模糊,還是先看個例子吧,我覺得看完例子,在看這段話肯定比較有感覺。
例 最長遞增字串
問題描述:http://en.wikipedia.org/wiki/Longest_increasing_subsequence_problem (其實顯而易見)
假設我的一串input是 X1,X2,X3,。。。,Xn,按下圖構造我們的樹(enumeration tree)。
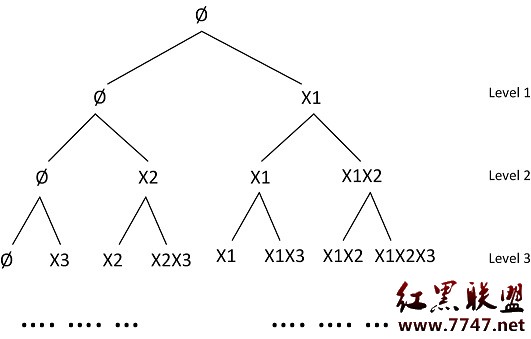
如何構造這棵樹通