先看一段來自wikipedia的定義:http://en.wikipedia.org/wiki/Divide_and_conquer_algorithm
Divide and conquer (D&C) is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same (or related) type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.
簡單翻譯一下:
分治算法是基於多分枝遞歸的一種算法設計模式。分治算法遞歸地把一個大問題分解為多個類型相同的子問題,直到這些子問題足夠的簡單能被直接解決。最後把這些子問題的解結合起來就能得到原始問題的解。
根據這個定義,我們可以很明顯的知道,對於D&C問題,我們解決它需要兩步,一是要找到遞歸式;二是要根據遞歸式能找到最後的答案。
首先,什麼是遞歸式。
下面是從算法導論(Introduction to Algorithm Edition 3)上copy下的一小段話,解釋的相當清楚。
Recurrences go hand in hand with the divide-and-conquer paradigm, because theygive us a natural way to characterize the running times of divide-and-conquer algorithms.A recurrence is an equation or inequality that describes a function in terms of its value on smaller inputs.
舉個例子,
T(n) = 4T(n/2) + n,這個表達式就是我們的遞歸式。
對於不同的問題,我們得到的遞歸式各不相同,通常這個是因問題而已。但總體思路是如何分解原始的問題。
而本文的重點則是在後面,介紹如何在有了遞歸式的情況下,找到問題的答案。如分析某個問題的時間復雜度。
通常,解決這類問題(一直遞歸式,找答案)有三種方法:
1. Mathematical Induction 數學歸納法
2. Recursion Tree 畫遞歸樹找規律
3. Master Theorem 主定理(好像中文版的算法導論上就是這樣翻譯的,感覺真挫)
後面就簡單針對以上三種方法用具體例子做一個簡單的說明。
1. Mathematical Induction 數學歸納法
使用數學歸納法,這個大家基本都清楚,就是假設一個在n的時候結論成立,證明在n+1的時候結論也成立,當然,在我們這裡,稍微有點變化。舉個例子。
T(n) = T(n/2) + T(n/4) + T(n/8) + n
現在我們要就上面表達式T(n),現在我們就先guess T(n) = Theta(n)。
當然我們知道要證明T(n) = Theta(n),我們需要分別證明T(n) = O(n)和T(n) = Omega(n)。
很顯然,這裡T(n) = Omega(n)的,因為T(n) = T(n/2) + T(n/4) + T(n/8) + n > n,顯然,T(n) = Omega(n).
下面用數學歸納法證明T(n) = O(n)
假設T(n) <= cn,所以其中c是一個常數。
所以T(n) <= c*n/2 + c*n/4 + c*n/8 + n = (7c/8+1)n
我們只需讓(7c/8+1)n <= cn,顯然我們可以找到一個正常數c使該式成立。所以T(n) = O(n)。
綜上,T(n) = Theta(n)。
上面的證明是沒有問題了,但是可能有朋友要問,憑什麼你一開始就guess T(n) = Theta(n) 呢?沒錯,make a good guess 是這種方法的關鍵,下面就簡單的說一下make this guess的intuition。
首先,我們可以簡單的畫出下面這棵樹。
================================================================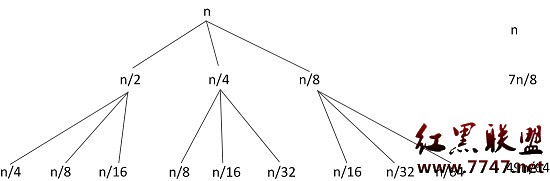 當然我們可以發現,在每一層,隨著遞歸的深入,每一層的總cost是減小的,所以我們可以推測,在層數很大的情況下,那一層的總cost很小,無法和頂層相比,這也就是說,這個問題的T(n)主要由頂層決定,最頂層是n,所以我們有理由guess答案是cn。c為一常數。
下面在介紹兩個guess的小tricks
1)遇到T(n) = aT(n/b + d) + f(n)的時候,在絕大多數的情況下,我們可以直接忽略d來進行guess,因為當n足夠大的時候 n/b + d 和 n/b 幾乎是一樣的。
2)guess的時候可以加一個常數項,比如上面guess T(n) = O(n)的時候,我們用的是 T(n)<= cn,有時候推導不順利的時候,可以試試 用T(n) <= cn-d,這樣可以擺脫一些常數項的干擾。
2. Recursion Tree 畫遞歸樹找規律
其實這個方法和前面的畫樹的方法很相似,這裡就舉一個簡單的例子來說明問題。
現在假設我們的遞歸式是 T(n) = aT(n/b) + n^k。 這裡由於畫樹比較麻煩(偷個懶(*^__^*) 。。。)我就畫成表格了,其實原理都一樣,只是呈現的方式不一樣。
當然我們可以發現,在每一層,隨著遞歸的深入,每一層的總cost是減小的,所以我們可以推測,在層數很大的情況下,那一層的總cost很小,無法和頂層相比,這也就是說,這個問題的T(n)主要由頂層決定,最頂層是n,所以我們有理由guess答案是cn。c為一常數。
下面在介紹兩個guess的小tricks
1)遇到T(n) = aT(n/b + d) + f(n)的時候,在絕大多數的情況下,我們可以直接忽略d來進行guess,因為當n足夠大的時候 n/b + d 和 n/b 幾乎是一樣的。
2)guess的時候可以加一個常數項,比如上面guess T(n) = O(n)的時候,我們用的是 T(n)<= cn,有時候推導不順利的時候,可以試試 用T(n) <= cn-d,這樣可以擺脫一些常數項的干擾。
2. Recursion Tree 畫遞歸樹找規律
其實這個方法和前面的畫樹的方法很相似,這裡就舉一個簡單的例子來說明問題。
現在假設我們的遞歸式是 T(n) = aT(n/b) + n^k。 這裡由於畫樹比較麻煩(偷個懶(*^__^*) 。。。)我就畫成表格了,其實原理都一樣,只是呈現的方式不一樣。
 當然,我們知道最後的level是 log_{b}^n,然後我們把最後一列相加,就得到了我們的結果,
當然,我們知道最後的level是 log_{b}^n,然後我們把最後一列相加,就得到了我們的結果,
 最後,再啰嗦一句。
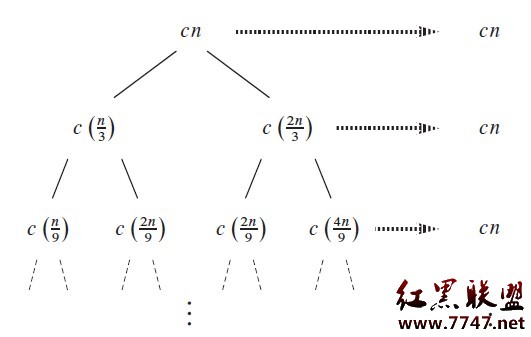
在找樹的高度height的時候,有時候可能我們會遇到 T(n) = T(n/3)+T(2n/3)+O(n)類似的問題,這個時候樹的高度可能不能一下子得到,其實我們如果畫出recursion tree,如下圖,可以知道,樹的高度有最長的那個分支決定,也就是n---(2/3)n---(2/3)^2n...---1這條分支,所以高度k 應該滿足 (2/3)^k * n = 1,所以k = log_{3/2}^{n}.
最後,再啰嗦一句。
在找樹的高度height的時候,有時候可能我們會遇到 T(n) = T(n/3)+T(2n/3)+O(n)類似的問題,這個時候樹的高度可能不能一下子得到,其實我們如果畫出recursion tree,如下圖,可以知道,樹的高度有最長的那個分支決定,也就是n---(2/3)n---(2/3)^2n...---1這條分支,所以高度k 應該滿足 (2/3)^k * n = 1,所以k = log_{3/2}^{n}.

3. Master Theorm 主定理
這個其實沒有什麼好講的,定理的證明比較復雜,感興趣的朋友可以直接查閱算法導論第四張最後幾個小節,這裡就把結論貼上來了。
通常,條件符合,就直接得結論。
