劉子韬
通常我們說到某個算法,我們經常關心他的時間復雜度,當然,我們通常關心的是這個時間復雜度的upper bound,即上界。upper bound告訴我們在某些很糟糕的情況下,我們的算法的性能。比如我們的基於比較的排序算法,我們知道mergesort(歸並排序)是O(nlgn),但是我們應該能提出這樣的疑問,can we do it better?(我們能做的更好嗎?) 所以,在這篇文章裡,我們將簡單介紹一下對於算法的下界,lower bound,它告訴我們對於某個問題,是否存在更好的算法。 lower bound告訴我們什麼不能做到。
"Lower bounds tell us what cannot be done, they are very important in guiding us in our search for what can be done."
(當然對於lower bound的問題,我自己是google了一下,中文方面的資料很少,據本人了解高校內算法課涉及lower bound的也幾乎沒有,但google本文上面的keywords,可以看到北美的各大高校基本全部都有相關知識章節,本科和研究生都有,莫非這就是教育的差異??!!這裡就權當一個入門的tutorial了)
回歸主題:
當然,我們知道,所謂lower bound,也就是找Omega(n)了。(不清楚的童鞋可以看一下文章開頭給的鏈接)
還是決定舉一個例子慢慢展開。
比如我們知道基於比較的排序算法最好也就是nlgn了,所以,這也就是說,我們應該能證明sorting = Omega(nlgn),當然,這裡的sorting是指任意的排序算法。這時我們就會發現,問題出來了,我們要證明任意算法都滿足一個條件,任意,任意....一些傳統的舉反例啊,針對某個算法的內部分析啊什麼的都不能用了。
對於找解決某一問題的那一類算法的lower bound,我們通常有兩種辦法,
1)decision tree 我們通過分析決策樹的方法來得到lower bound(這也是算法導論裡面提到的方法)
2)adversary strategy 這個確實不好翻譯,競爭者策略?! 當然這個方法要比上面的decision tree得到的lower bound更tight一些。(當然這個也不絕對,還要看你的strategy)
鑒於基本上lower bound的引入都是通過sorting這個人神共知的algorithm引入的,我這裡也不非主流了。
下面先用sorting的lower bound的例子來分別解釋一下上面提到的兩個方法,然後在舉一些例子幫助大家加深理解。恩。就這樣。
Lets get started~
對於基於比較的排序,我們知道,這裡排序的依據是比較!(這真是句大實話,同時也是句廢話O(∩_∩)O~)
現在假設我們待比較的數據是 a1,a2,...,an,我們知道對於這n個數據(假設裡面沒有相等的元素),我們可以對這n個數據做一個全排列,裡面有n!種。那麼什麼是decision tree呢?偷個懶,截了個算法導論的圖。
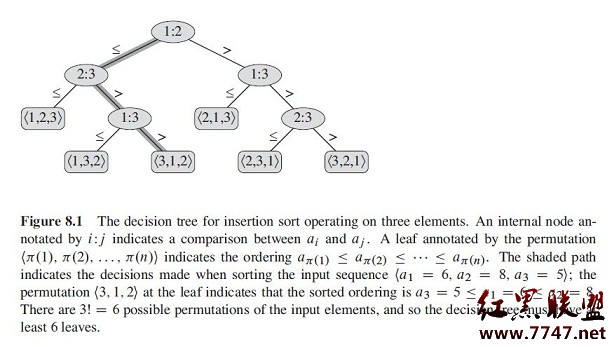
專門截了那麼一大段文字,因為講的很詳細,希望不太明白的童鞋都先仔細看了再說。每個非葉子節點的數字可以想象成待比較的元素ai的下標i,其中root表示比較a1和a2,如果是小於走左枝,大於走右枝。下面類似。對於葉子節點,就是一個最後的算有元素下標的全排列,當然這也就是一個可能的最後的排序的結果了。這個應該還是很好理解的,不好理解的我在啰嗦一句,比如 輸入是a1,a2,a3,a4, 我最後有個葉子節點是 [ 2 4 1 3],這也就表示最後的排序結果是a2,a4,a1,a3。
這棵樹看起來很簡單,當然,他還是能給我很多有用的信息的,首先我們知道比較算法的復雜度和進行比較的次數緊密相關的。我們可以從樹上看出,從root到leaf,一路上經歷的比較次數,就是我們這個分支的高度,當然,很明顯,我們是要考慮這棵樹的最大的高度,也就是最長的那支。它表示了在最壞的情況下,我們需要的比較次數(這裡好像和樹的高度的offical的定義有沖突了,明白意思就好O(∩_∩)O~)
好,現在我們就開始找lower bound了~很顯然,我們這棵樹是二叉的,大於向左,小於向右,我們最後的高度是h,我們知道完全二叉樹高為h的葉子最多有2^h個,同時我們也是到n個數據,最多有n!個排列,所以根據我們的decision tree,我們可以得到:
n! <= 2^h
當然簡單變形一下,h>= lg(n!)
所以 h = Omega(nlgn)。(不明真相的童鞋請看開頭給的鏈接,裡面有一些basic的數學公式)
這說明了什麼,這說明了對於基於比較的排序算法,我們至少需要Omega(nlgn)次比較,不然最下面那支的葉子節點的結果我們就得不到。當然,最重要的的是,我們這裡得出的結論是對於任意的排序算法,任意的哦!
下面再來看看如何利用Adversary Strategy來得到這個lower bound。
首先解釋一下Adversary Strategy的思路:
我們可以想象存在一個Adversary,當然我們中文裡應該就叫神~有這麼一個神,當我們在進行比較的時候,我們不能立刻得到比較的結果,我們要去問神,只有神知道,(神的力量無法無天....跑了....回到主題),每當我們要進行比較,都要從神那裡得到比較的結果。
當然對於神來說,它總是希望拖延我們,然後盡量多的詢問它 關於比較的結果。 所以在我們和神直接就存在了一種adversarial的關系。
針對於sorting,我們知道一共有n!種可能,比如a1,a2,a3,我們的可能的結果有[1 2 3] [1 3 2] [2 1 3] [2 3 1] [ 3 1 2 ] [ 3 2 1 ],姑且叫它候選集合S,每當我們從神的那裡得到兩個數據的比較結果之後,我們就可以從候選集合中剔除若干元素,縮小候選集合的大小|S|,當|S|=1的時候,我們的任務就完成了。而神要做的是什麼呢?神要做的就是他每次都要告訴我們一個結果,但是它總是想盡力的讓我們的候選集合剩下的元素盡可能的多。不難看出,每次都讓我們剩下的size大於等於前一次的一般,也就是我們每從神那裡得到一個答案後,最多把候選集合裡面的東西砍掉一般。所以為了讓|S|從n!到1,我們至少需要問lg(n!)次,所以lower bound是Omega(nlgn)。當然如果我們沒有問到nlgn次,我們的候選集合裡面至少有兩個元素,這時候算法要給出一個結果,而神總會說答案是另外的,這樣我們的算法就fail了,這也就說明了小於nlgn的都是不行的。(有點類似反證)
上面證明了sorting的在worst case下的lower bound,下面我們還可以附帶證明在average case的情況下,sorting的lower bound也是Omega(nlgn)。
其實通過上面的decision tree的方法,我們已經知道,找average case下的lower bound,其實也就是找那棵樹的所有分支高度的平均值的lower bound。
如果我們的樹是平衡二叉樹,我們知道,每個分支都是nlgn,所以average case的lower bound就是Omega(nlgn),但是對於根據比較得到的decision tree不是平衡二叉樹呢?其實我們只要證明 the one that minimizes their average depth is a completely balanced tree。這個其實也很顯然,如果不是平衡二叉樹,說明最深的節點減去最淺的節點的高度差大於等於二,這時我們可以把最深的那兩個節點移接到最淺的那支上,這樣我們減小了average heights,但是沒有影響到別的,這也就說明了只有對於任何不平衡的樹,我們都可以使他的average height更小一些,所以也就說明了average depth of leaves must be at least nlgn。證畢。
順便可以證明一下對於所有的randomized sorting algorithm,比較次數的lower bound也是nlgn。http://en.wikipedia.org/wiki/Randomized_algorithm
決定把這個放到下一篇文章中講。O(∩_∩)O~
後面舉幾個例子來簡單具體闡述一下上面說的兩個方法。
例 有兩個長度為n的已經排好的list,a1<a2<...<an, b1<b2<...<bn,我們要把這兩個list合並到一個list裡面,保證這個list是increasing的,要證明在合並的過程中比較次數的lower bound是 2n-1.
假設我們用adversarial strategy證明,假設我們只比較了2n-2次,也就是我們只想神詢問了2n-2次,這時我們知道有一個元素ai,他一定是沒有和bj或者是bj+1比較的,假設我們的ai = 2i-1,也就是所有的奇數,bi = 2i,所有的偶數,那麼這個時候,我們的算法已經給出了output,但是對於無所不能的神來說,它知道你沒有比較ai和bj或者是沒有比較ai和bj+1。
如果你沒有比較ai和bi,你輸出的是aibi,但是神可以交換ai和bi的值,這個時候ai = 2i,bi = 2i-1,交換的同時,依然保證a1<a2<...<an, b1<b2<...<bn,所以這個時候,你的算法錯了。
同理,如果你沒有比較ai和bi+1,神依舊可以交換ai和bj+1的值,導致你的算法還是錯的,所以你的2n-2的算法悲劇了,所以證明lower bound是2n-1。
例 給定一個長度為n的已經排好的list,a1<a2<...<an, 和一個數x,要找這個list裡面有沒有一個ai,ai==x。 給一個比較次數的lower bound,並證明。
這個我們可以用decision tree的方法找到這個lower bound,考慮下面的decision tree:
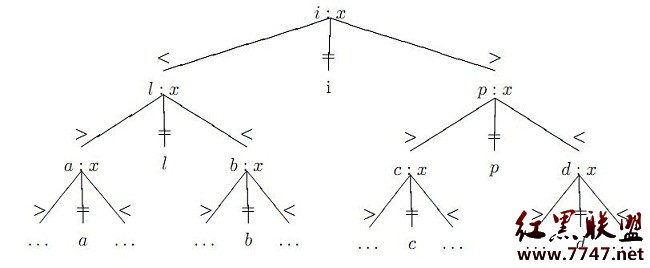
從這個樹上我們可以得出:
1)對於每一個非葉子節點,都有兩個分支。
2)這個樹一共有n個葉子節點(對應了我們n個可能的答案)
假設樹的高度是h,我們知道最多可能出現的葉子節點數是 2^0+2^1+2^2+。。。+2^k-1,這是等於2^k-1的,當然,這個是大於等於n的,所以,就有 2^k-1 >=n, 可以得到 k >= lg(n+1),這也就是,一路比較下去我們至少要用 lg(n+1)次比較。