歐幾裡德算法（C語言）

俠客行
#include <stdio.h>
void luwei_gcd(int a,int b,int &d,int &x,int &y )
{
        if(b==0) //對於ax+by=d且b=0,顯然有x=1(因為gcd(a,b) = d,可知a=d)
        {
                d=a;
                x=1;
                y=0;
                return ;
        }
        luwei_gcd(b,a%b,d,y,x);//a*x+b*y=d可轉化為b*y+(a%b)*(y-x*(a/b))=d
        y -= x * (a/b) ;//在回溯時x = y,y = y-x*(a/b),更新x,y的值
}
// ax ≡ 1 (mod n) 滿足gcd(a,n) = 1,該問題可化為ax + bn = 1,然後上面的函數，即可求出x
int shuchu (int a ,int n)
{
        int d,x,y ;
        luwei_gcd(a,n,d,x,y);
        if(d==1) //ax + bn = 1
        {
                x=x%n;
                if(x<0)
               return (x+n)%n;//返回的值保證是正數
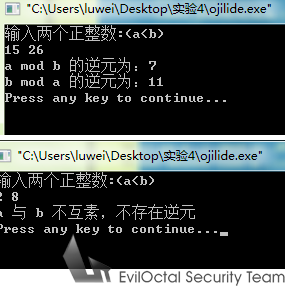
               printf("a mod b 的逆元為：%dn",x);
               printf("b mod a 的逆元為：%dn",(1-a*(x-26))/n);
        }
        else
                printf("a 與 b 不互素，不存在逆元n");
}

int main()
{
    int a,b;
    printf("輸入兩個正整數:(a<b)n");
    scanf("%d%d",&a,&b);
    shuchu(a,b);
    return 0;
}