原來打算把算法導論在7月份前搞定,現在已經過去一個多月了,才只看到第15章,後面也只零散看了一些,不知道假期前能否看完。。。夠嗆啊,馬上要期末考試了,上學期GPA不到2,被學位警告了,雖說以後不學這個專業了,但起碼成績單上也不能有掛科是吧。。。要是平時一點不看,考前靠春哥,曾哥,關公哥都不行啊。。。這進度,郁悶!
盡力吧!
順便還是說兩句話:
1.有些書上分析的相當好了,我不想做畫蛇添足的人,所以有的地方我會適當省略,當然也不是說我總結的地方就是書上講的不好的地方,只是沒人有一套自己的理解方式,我用自己的話去總結了,當時也就是最適合我的知識!所以,建議大家多寫一些算法總結,你會體會到好處的!
2.而且我這個的性質是總結,不是對一個算法的具體講解,所以不先看書,大家應該讀不懂的,就比如下面,題目我就沒有貼出來,大家不看數,肯定就讀不懂,我的目的是大家看完書後,謝謝總結,或者看看別人寫的總結,說不定可以發現自己哪些地方理解錯了,哪些地方不理解,或是哪些地方值得探討。
這一次主要是分析15.1節的例子—裝配線調度問題。
題目有點長,首先得把題目讀懂。
這個例子書上花了6面紙的篇幅來詳細分析,由此可見其重要性。
談到DP,不得不說的就是暴力法,大家都知道,如果用暴力解決類似問題,一般時間復雜度都是非常非常的高,這個時候救世主DP就出來了,DP以避免了許多重復的計算,而大大降低了時間復雜度。
按照書上的四個步驟,我在這裡提取一些重點,建議還是把P194~196這四步完整步驟看書上的分析。只有慢慢品味,你才會發現《算法導論》的美。
步驟一:
分析問題,比如一個底盤要到達S[1][j],則有兩種情況,第一種是從S[1][j-1]到S[1][j],第二種是從S[2][j-1]到S[1][j]。找出這兩者所花時間的最小,則就是S[1][j]所需時間的最小。
這就是有局部最優解求全局最優解。也就是說,一個問題的最優解包含了子問題的一個最優解。我們稱這個性質為最優子結構。這是是否可以應用DP的標志之一。
步驟二:
找出這個遞歸關系,由步驟一可以得到這個遞歸關系:
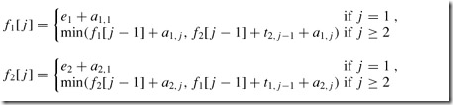
步驟三:
因為遞歸的關系,一般總是可以轉換為非遞歸的算法。
由已知量f1[1], f2[1]逐步推出未知量,推啊推,推啊推,最後就推到結果了~~~~
步驟四:
再由已知結果返回求路徑。
這一節最給力的就是這個例子以及相應的圖:
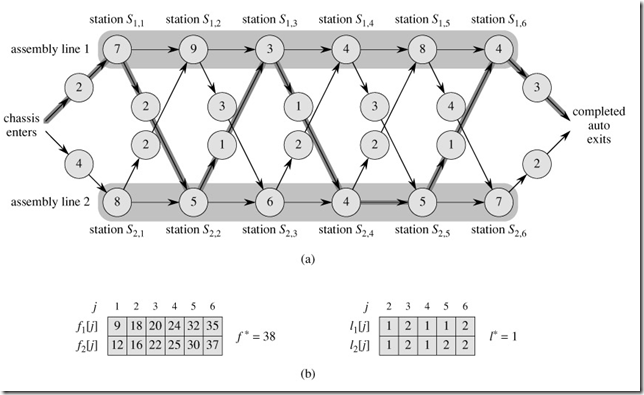
拿起筆,用書上給出的例子,分析這個圖!
以下是代碼:
/*
Author: Tanky Woo
Blog: www.WuTianQi.com
About: 《算法導論》15.1 裝配線調度
*/
#include <iostream>
using namespace std;
int n; // 一個裝配線上有n個裝配站
int e1, e2; // 進入裝配線1,2需要的時間
int x1, x2; // 離開裝配線1,2需要的時間
int t[3][100]; // t[1][j]表示底盤從S[1][j]移動到S[2][j+1]所需時間,同理t[2][j]
int a[3][100]; // a[1][j]表示在裝配站S[1][j]所需時間
int f1[100], f2[100]; // f1[j], f2[j]分別表示在第一/第二條裝配線上第j個裝配站的最優解
int ln1[100], ln2[100];// ln1[j]記錄第一條裝配線上,最優解時第j個裝配站的前一個裝配站是第一條線還是第二條線上
int f, ln; // 最優解是,f代表最小花費時間,ln表示最後出來時是從裝配線1還是裝配線2
void DP()
{
f1[1] = e1 + a[1][1];
f2[1] = e2 + a[2][1];
for(int j=2; j<=n; ++j)
{
// 處理第一條裝配線的最優子結構
if(f1[j-1] + a[1][j] <= f2[j-1] + t[2][j-1] + a[1][j])
{
f1[j] = f1[j-1] + a[1][j];
ln1[j] = 1;
}
else
{
f1[j] = f2[j-1] + t[2][j-1] + a[1][j];
ln1[j] = 2;
}
// 處理第二條裝配線的最優子結構
if(f2[j-1] + a[2][j] <= f1[j-1] + t[1][j-1] + a[2][j])
{
f2[j] = f2[j-1] + a[2][j];
ln2[j] = 2;
}
else
{
f2[j] = f1[j-1] + t[1][j-1] + a[2][j];
ln2[j] = 1;
}
}
if(f1[n] + x1 <= f2[n] + x2)
{
f = f1[n] + x1;
ln = 1;
}
else
{
f = f2[n] + x2;
ln = 2;
}
}
void PrintStation()
{
int i= ln;
cout << "line " << i << ", station " << n << endl;
for(int j=n; j>=2; --j)
{
if(i == 1)
i = ln1[j];
else
i = ln2[j];
cout << "line " << i << ", station " << j-1 << endl;
}
}
int main()
{
//freopen("input.txt", "r", stdin);
cout << "輸入裝配站的個數: ";
cin >> n;
cout << "輸入進入裝配線1,2所需的時間e1, e2 :";
cin >> e1 >> e2;
cout << "輸入離開裝配線1, 2所需的時間x1, x2: ";
cin >> x1 >> x2;
cout << "輸入裝配線1上各站加工所需時間a[1][j]: ";
for(int i=1; i<=n; ++i)
cin >> a[1][i];
cout << "輸入裝配線2上各站加工所需時間a[2][j]: ";
for(int i=1; i<=n; ++i)
cin >> a[2][i];
cout << "輸入裝配線1上的站到裝配線2上的站所需時間t[1][j]: ";
//注意這裡是i<n,不是i<=n
for(int i=1; i<n; ++i)
cin >> t[1][i];
cout << "輸入裝配線2上的站到裝配線1上的站所需時間t[2][j]: ";
for(int i=1; i<n; ++i)
cin >> t[2][i];
DP();
cout << "最快需要時間: " << f << endl;
cout << "路線是: " << endl;
PrintStation();
cout << endl;
}
最後還是要感歎一下,《算法導論》講的真是棒極了,希望大家能靜下心把這一章節好好看看