尋找最小的k個數
題目描述:5.查找最小的k個元素
題目:輸入n個整數,輸出其中最小的k個。
例如輸入1,2,3,4,5,6,7和8這8個數字,則最小的4個數字為1,2,3和4。
第一節、各種思路,各種選擇
0、 咱們先簡單的理解,要求一個序列中最小的k個數,按照慣有的思維方式,很簡單,先對這個序列從小到大排序,然後輸出前面的最小的k個數即可。
1、 至於選取什麼的排序方法,我想你可能會第一時間想到快速排序,我們知道,快速排序平均所費時間為n*logn,然後再遍歷序列中前k個元素輸出,即可,總的時間復雜度為O(n*logn+k)=O(n*logn)。
2、 咱們再進一步想想,題目並沒有要求要查找的k個數,甚至後n-k個數是有序的,既然如此,咱們又何必對所有的n個數都進行排序列?
這時,咱們想到了用選擇或交換排序,即遍歷n個數,先把最先遍歷到得k個數存入大小為k的數組之中,對這k個數,利用選擇或交換排序,找到k個數中的最大數kmax(kmax設為k個元素的數組中最大元素),用時O(k)(你應該知道,插入或選擇排序查找操作需要O(k)的時間),後再繼續遍歷後n-k個數,x與kmax比較:如果x<kmax,則x代替kmax,並再次重新找出k個元素的數組中最大元素kmax‘(多謝kk791159796 提醒修正);如果x>kmax,則不更新數組。這樣,每次更新或不更新數組的所用的時間為O(k)或O(0),整趟下來,總的時間復雜度平均下來為:n*O(k)=O(n*k)。
3、 當然,更好的辦法是維護k個元素的最大堆,原理與上述第2個方案一致,即用容量為k的最大堆存儲最先遍歷到的k個數,並假設它們即是最小的k個數,建堆費時O(k)後,有k1<k2<...<kmax(kmax設為大頂堆中最大元素)。繼續遍歷數列,每次遍歷一個元素x,與堆頂元素比較,x<kmax,更新堆(用時logk),否則不更新堆。這樣下來,總費時O(k+(n-k)*logk)=O(n*logk)。此方法得益於在堆中,查找等各項操作時間復雜度均為logk(不然,就如上述思路2所述:直接用數組也可以找出前k個小的元素,用時O(n*k))。
4、 按編程之美第141頁上解法二的所述,類似快速排序的劃分方法,N個數存儲在數組S中,再從數組中隨機選取一個數X(隨機選取樞紐元,可做到線性期望時間O(N)的復雜度,在第二節論述),把數組劃分為Sa和Sb倆部分,Sa<=X<=Sb,如果要查找的k個元素小於Sa的元素個數,則返回Sa中較小的k個元素,否則返回Sa中k個小的元素+Sb中小的k-|Sa|個元素。像上述過程一樣,這個運用類似快速排序的partition的快速選擇SELECT算法尋找最小的k個元素,在最壞情況下亦能做到O(N)的復雜度。不過值得一提的是,這個快速選擇SELECT算法是選取數組中“中位數的中位數”作為樞紐元,而非隨機選取樞紐元。
5、 RANDOMIZED-SELECT,每次都是隨機選取數列中的一個元素作為主元,在0(n)的時間內找到第k小的元素,然後遍歷輸出前面的k個小的元素。 如果能的話,那麼總的時間復雜度為線性期望時間:O(n+k)=O(n)(當k比較小時)。
Ok,稍後第二節中,我會具體給出RANDOMIZED-SELECT(A, p, r, i)的整體完整偽碼。在此之前,要明確一個問題:我們通常所熟知的快速排序是以固定的第一個或最後一個元素作為主元,每次遞歸劃分都是不均等的,最後的平均時間復雜度為:O(n*logn),但RANDOMIZED-SELECT與普通的快速排序不同的是,每次遞歸都是隨機選擇序列從第一個到最後一個元素中任一一個作為主元。
6、 線性時間的排序,即計數排序,時間復雜度雖能達到O(n),但限制條件太多,不常用。
7、 updated: huaye502在本文的評論下指出:“可以用最小堆初始化數組,然後取這個優先隊列前k個值。復雜度O(n)+k*O(log n)”。huaye502的意思是針對整個數組序列建最小堆,建堆所用時間為O(n)(算法導論一書上第6章第6.3節已經論證,在線性時間內,能將一個無序的數組建成一個最小堆),然後取堆中的前k個數,總的時間復雜度即為:O(n+k*logn)。
關於上述第7點思路的繼續闡述:至於思路7的O(n+k*logn)是否小於上述思路3的O(n*logk),即O(n+k*logn)?< O(n*logk)。粗略數學證明可參看如下第一幅圖,我們可以這麼解決:當k是常數,n趨向於無窮大時,求(n*logk)/(n+k*logn)的極限T,如果T>1,那麼可得O(n*logk)>O(n+k*logn),也就是O(n+k*logn)< O(n*logk)。雖然這有違我們慣常的思維,然事實最終證明的確如此,這個極值T=logk>1,即采取建立n個元素的最小堆後取其前k個數的方法的復雜度小於采取常規的建立k個元素最大堆後通過比較尋找最小的k個數的方法的復雜度。但,最重要的是,如果建立n個元素的最小堆的話,那麼其空間復雜度勢必為O(N),而建立k個元素的最大堆的空間復雜度為O(k)。所以,綜合考慮,我們一般還是選擇用建立k個元素的最大堆的方法解決此類尋找最小的k個數的問題。
也可以如gbb21所述粗略證明:要證原式k+n*logk-n-k*logn>0,等價於證(logk-1)n-k*logn+k>0。當when n -> +inf(n趨向於正無窮大)時,logk-1-0-0>0,即只要滿足logk-1>0即可。原式得證。即O(k+n*logk)>O(n+k*logn) => O(n+k*logn)< O(n*logk),與上面得到的結論一致。
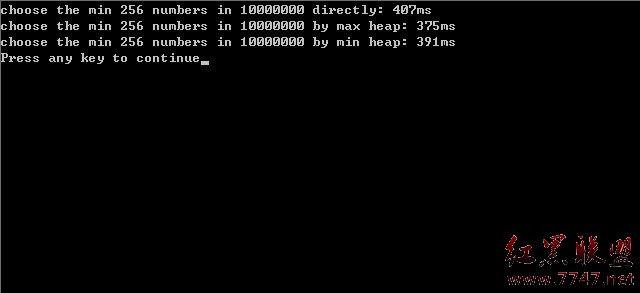
事實上,是建立最大堆還是建立最小堆,其實際的程序運行時間相差並不大,運行時間都在一個數量級上。因為後續,我們還專門寫了個程序進行測試,即針對1000w的數據尋找其中最小的k個數的問題,采取兩種實現,一是采取常規的建立k個元素最大堆後通過比較尋找最小的k個數的方案,一是采取建立n個元素的最小堆,然後取其前k個數的方法,發現兩相比較,運行時間實際上相差無幾。結果可看下面的第二幅圖。

8、 @lingyun310:與上述思路7類似,不同的是在對元素數組原地建最小堆O(n)後,然後提取K次,但是每次提取時,換到頂部的元素只需要下移頂多k次就足夠了,下移次數逐次減少(而上述思路7每次提取都需要logn,所以提取k次,思路7需要k*logn。而本思路8只需要K^2)。此種方法的復雜度為O(n+k^2)。@July:對於這個O(n+k^2)的復雜度,我相當懷疑。因為據我所知,n個元素的堆,堆中任何一項操作的復雜度皆為logn,所以按理說,lingyun310方法的復雜度應該跟下述思路8一樣,也為O(n+k*logn),而非O(n+k*k)。ok,先放到這,待時間考證。06.02。
updated:
經過和幾個朋友的討論,已經證實,上述思路7lingyun310所述的思路應該是完全可以的。下面,我來具體解釋下他的這種方法。
我們知道,n個元素的最小堆中,可以先取出堆頂元素得到我們第1小的元素,然後把堆中最後一個元素(較大的元素)上移至堆頂,成為新的堆頂元素(取出堆頂元素之後,把堆中下面的最後一個元素送到堆頂的過程可以參考下面的第一幅圖。至於為什麼是怎麼做,為什麼是把最後一個元素送到堆頂成為堆頂元素,而不是把原來堆頂元素的兒子送到堆頂呢?具體原因可參考相關書籍)。
此時,堆的性質已經被破壞了,所以此後要調整堆。怎麼調整呢?就是一般人所說的針對新的堆頂元素shiftdown,逐步下移(因為新的堆頂元素由最後一個元素而來,比較大嘛,既然是最小堆,當然大的元素就要下沉到堆的下部了)。下沉多少步呢?即如lingyun310所說的,下沉k次就足夠了。
下移k次之後,此時的堆頂元素已經是我們要找的第2小的元素。然後,取出這個第2小的元素(堆頂元素),再次把堆中的最後一個元素送到堆頂,又經過k-1次下移之後(此後下移次數逐步減少,k-2,k-3,...k=0後算法中斷)....,如此重復k-1趟操作,不斷取出的堆頂元素即是我們要找的最小的k個數。雖然上述算法中斷後整個堆已經不是最小堆了,但是求得的k個最小元素已經滿足我們題目所要求的了,就是說已經找到了最小的k個數,那麼其它的咱們不管了。
我可以再舉一個形象易懂的例子。你可以想象在一個水桶中,有很多的氣泡,這些氣泡從上到下,總體的趨勢是逐漸增大的,但卻不是嚴格的逐次大(正好這也符合最小堆的性質)。ok,現在我們取出第一個氣泡,那這個氣泡一定是水桶中所有氣泡中最小的,把它取出來,然後把最下面的那個大氣泡(但不一定是最大的氣泡)移到最上面去,此時違反了氣泡從上到下總體上逐步變大的趨勢,所以,要把這個大氣泡往下沉,下沉到哪個位置呢?就是下沉k次。下沉k次後,最上面的氣泡已經肯定是最小的氣泡了,把他再次取出。然後又將最下面最後的那個氣泡移至最上面,移到最上面後,再次讓它逐次下沉,下沉k-1次...,如此循環往復,最終取到最小