前奏
本章陸續開始,除了繼續保持原有的字符串、數組等面試題之外,會有意識的間斷性節選一些有關數字趣味小而巧的面試題目,重在突出思路的“巧”,和“妙”。本章親和數問題之關鍵字,“500萬”,“線性復雜度”。
第一節、親和數問題
題目描述:
求500萬以內的所有親和數
如果兩個數a和b,a的所有真因數之和等於b,b的所有真因數之和等於a,則稱a,b是一對親和數。
例如220和284,1184和1210,2620和2924。
分析:
首先得明確到底是什麼是親和數?
親和數問題最早是由畢達哥拉斯學派發現和研究的。他們在研究數字的規律的時候發現有以下性質特點的兩個數:
220的真因子是:1、2、4、5、10、11、20、22、44、55、110;
284的真因子是:1、2、4、71、142。
而這兩個數恰恰等於對方的真因子各自加起來的和(sum[i]表示數i 的各個真因子的和),即
220=1+2+4+71+142=sum[284],
284=1+2+4+5+10+11+20+22+44+55+110=sum[220]。
得284的真因子之和sum[284]=220,且220的真因子之和sum[220]=284,即有sum[220]=sum[sum[284]]=284。
如此,是否已看出絲毫端倪?
如上所示,考慮到1是每個整數的因子,把出去整數本身之外的所有因子叫做這個數的“真因子”。如果兩個整數,其中每一個真因子的和都恰好等於另一個數,那麼這兩個數,就構成一對“親和數”
求解:
了解了什麼是親和數,接下來咱們一步一步來解決上面提出的問題(以下內容大部引自水的原話,同時水哥有一句原話,“在你真正弄弄懂這個范例之前,你不配說你懂數據結構和算法”)。
看到這個問題後,第一想法是什麼?模擬搜索+剪枝?回溯?時間復雜度有多大?其中bn為an的偽親和數,即bn是an的真因數之和大約是多少?至少是10^13(@iicup:N^1.5 對於5*10^6 , 次數大致 10^10 而不是 10^13.)的數量級的。那麼對於每秒千萬次運算的計算機來說,大概在1000多天也就是3年內就可以搞定了(iicup的計算: 10^13 / 10^7 =1000000(秒) 大約 278 小時. )。如果是基於這個基數在優化,你無法在一天內得到結果的。
一個不錯的算法應該在半小時之內搞定這個問題,當然這樣的算法有很多。節約時間的做法是可以生成伴隨數組,也就是空間換時間,但是那樣,空間代價太大,因為數據規模龐大。
在稍後的算法中,依然使用的伴隨數組,只不過,因為題目的特殊性,只是它方便和巧妙地利用了下標作為伴隨數組,來節約時間。同時,將回溯的思想換成遞推的思想(預處理數組的時間復雜度為logN(調和級數)*N,掃描數組的時間復雜度為線性O(N)。所以,總的時間復雜度為O(N*logN+N)(其中logN為調和級數) )。
第二節、伴隨數組線性遍歷
依據上文中的第3點思路,編寫如下代碼:
view plaincopy to clipboardprint?
//求解親和數問題
//第一個for和第二個for循環是logn(調和級數)*N次遍歷,第三個for循環掃描O(N)。
//所以總的時間復雜度為 O(n*logn)+O(n)=O(N*logN)(其中logN為調和級數)。
//關於第一個for和第二個for尋找中,調和級數的說明:
//比如給2的倍數加2,那麼應該是 n/2次,3的倍數加3 應該是 n/3次,...
//那麼其實就是n*(1+1/2+1/3+1/4+...1/(n/2))=n*(調和級數)=n*logn。
//copyright@ 上善若水
//July、updated,2011.05.24。
#include<stdio.h>
int sum[5000010]; //為防越界
int main()
{
int i, j;
for (i = 0; i <= 5000000; i++)
sum[i] = 1; //1是所有數的真因數所以全部置1
for (i = 2; i + i <= 5000000; i++) //預處理,預處理是logN(調和級數)*N。
//@litaoye:調和級數1/2 + 1/3 + 1/4......的和近似為ln(n),
//因此O(n *(1/2 + 1/3 + 1/4......)) = O(n * ln(n)) = O(N*log(N))。
{
//5000000以下最大的真因數是不超過它的一半的
j = i + i; //因為真因數,所以不能算本身,所以從它的2倍開始
while (j <= 5000000)
{
//將所有i的倍數的位置上加i
sum[j] += i;
j += i;
}
}
for (i = 220; i <= 5000000; i++) //掃描,O(N)。
{
// 一次遍歷,因為知道最小是220和284因此從220開始
if (sum[i] > i && sum[i] <= 5000000 && sum[sum[i]] == i)
{
//去重,不越界,滿足親和
printf("%d %d
",i,sum[i]);
}
}
return 0;
}
運行結果:
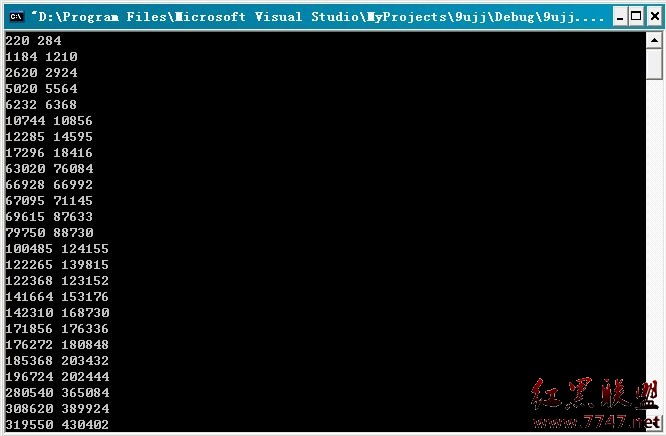
@上善若水:
1、可能大家理解的還不是很清晰,我們建立一個5 000 000 的數組,從1到2 500 000 開