說到貪心算法,避免不了於DP對比,所以前面的DP要了解。
貪心算法是使所做的選擇看起來都是當前最佳的,期望通過所做的局部最優選擇來產生一個全局最優解。
依然和上一章總結DP一樣,我先給出一個最容易入門的例子,來看看神馬是貪心?(是人就會貪心,這個算法很人性化啊
=。=)
一個最簡單的例子:
部分背包問題:
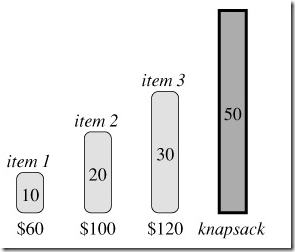
有N個物品,第i個物品價值vi,重wi,現在你有一個可以裝W 磅的包,你可以選擇帶走每個物品的全部或一部分,求如何選擇可以使背包所裝的價值最大?(這個是不是和前面DP中講的01背包很像?認真看清楚兩者題目的不同!)
假如有三種物品,背包可裝50磅的物品,物品1重10磅,價值60元;物品2重20磅,價值100元;物品3重30磅,價值120元。因此,既然可以選擇只裝一部分,我們可以算出每種物品的單位價值,物品1是每磅6元,物品2是美邦5元,物品3是每磅4元。按照貪心策略,應該現狀物品1,如果裝完物品1背包還有空間,再裝物品2……
最後的結果是:
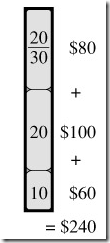
而如果按01背包,則結果是:
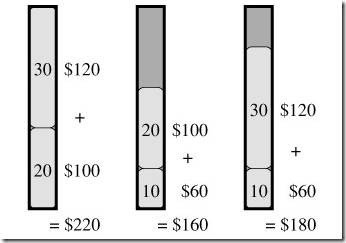
有興趣的可以拿我那01背包的程序去驗證這個結果。
下面是一個部分背包的小程序:
#include <iostream>
#include <algorithm>
using namespace std;
typedef struct Thing{
double v; // value
double w; // weight
}Thing;
Thing arr[100];
int n;
double W;
bool cmp(Thing a, Thing b)
{
return a.v/a.w > b.v/b.w;
}
int main()
{
cout << "輸入物品個數: ";
cin >> n;
cout << "輸入背包可載重量: ";
cin >> W;
cout << "輸入" << n << "個物品的價值和重量:" << endl;
for(int i=0; i<n; ++i)
cin >> arr[i].v >> arr[i].w;
sort(arr, arr+n, cmp);
int k = 0;
double value = 0;
while(W)
{
if(W >= arr[k].w)
{
W -= arr[k].w;
value += arr[k].v;
}
else
{
value += W * arr[k].v / arr[k].w;
W = 0;
}
++k;
}
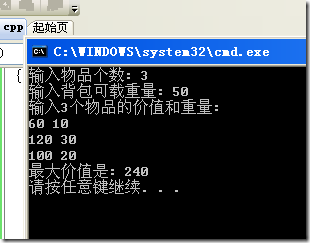
cout << "最大價值是: " << value << endl;
return 0;
}
結果如圖: