通過一個小程序,說明什麼是堆?"堆"這個詞最初是在堆排序中提出的,但後來就逐漸指"廢料收集存儲區",當然這裡不是指"廢料收集存儲區"。堆數據結構是一種數組對象,由於一棵完全二叉樹可以用一組地址連續的存儲單元依次自上而下、自左至右存儲,故堆可以被視為一棵完全二叉樹,如下圖:
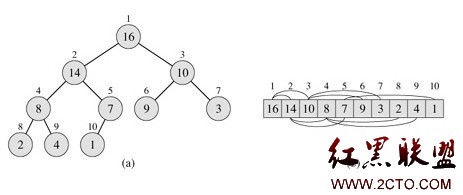
圓圈中的數字表示樹中每個節點的值,節點上方的數字表示對應的數組下標。
一個堆的數組A,用length[A]表述數組中的元素個數,heap-size[A]表示本身存放在A中的堆的元素個數,很明顯heap-size[A]<=length[A]。
樹的根為A[1],給定某個節點的下標i,很容易計算出其父節點PARENT(i)、左孩子LEFT(i)、右孩子RIGHT(i)的下標:
PARENT(i) --- i/2 LEFT(i) --- 2i RIGHT(i) --- 2i+1
二叉堆有兩種:最大堆和最小堆。最大堆滿足以下條件:除了根節點以外的每個節點i,有A[PARENT(i)]>=A[i]。即某個節點的值至多和父節點的值一樣大,也就是說,在以節點i為根節點的子樹中,其子節點的值都不大於該節點的值,由此可得出結論,最大堆根節點的值即是數組A的最大值。最小堆的概念正相反。
堆排序算法使用的是最大堆。下面介紹幾個堆排序使用的基本過程:
max_heapify過程,運行時間為O(lg n),它是保持最大堆性質的關鍵
build_max_heap過程,線性時間運行,在無序的數組基礎上構造最大堆
heapsort過程,運行時間為O(lg n),對一個數組原地進行排序
保持堆的性質 max_heapify算法如下:
max_heapify(A,i)
l ← LEFT(i)
r ← RIGHT(i)
if l ≤ heap-size[A] and A[l] > A[i]
then largest ← l
else largest ← i
if r ≤ heap-size[A] and A[r] > A[largest]
then largest ← r
if i ≠ largest
then exchange A[i] <-> A[largest]
max_heapify(A,largest)
如上述算法描述,首先在數組元素A[i],其左孩子為A[LEFT(i)],右孩子為A[RIGHT(i)]中找到最大的那個,將其下標值存儲到變量largest中。如果A[i]已經是最大值,則算法結束,否則A[i]與A[largest]交換,從而使節點i及其子節點滿足最大堆的性質。此時,以largest節點為根的子樹可能違反最大堆的性質,所以需要對該子樹遞歸調用max_heapify。下圖展示了這個過程:
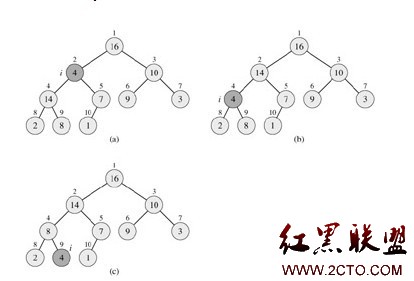
該圖展示的是max_heapify(A,2)的過程,讀者可參考算法自行理解該過程。
建堆 build_max_heap算法如下:
build_max_heap(A)
heap-size[A] ← length[A]
for i ← length[A]/2 downto 1
do max_heapify(A,i)
當用數組表示存儲了n個元素的堆時,可以證明葉子的下標是n/2+1,n/2+2,...,n。
假設第i個節點是堆中最後一個擁有葉子的節點,則它的節點必定是其左孩子(根據完全二叉樹的定義可得) ,則LEFT(i)=2i=n,即其左孩子在數組裡的存儲位置為n,可得i=n/2,所以從第i+1開始的節點沒有子節點,即n/2+1,n/2+2,...,n存儲的節點是葉子。
所以build_max_heap算法從第length[A]/2個節點往前開始調用max_heapify來建立最大堆,無需在葉子節點上調用max_heapify。下圖是此過程的展示:
堆排序 heapsort算法如下:
heapsort(A)
build_max_heap(A)
for i ← length[A] downto 2
do exchange A[1] <-> A[i]
heap-size[A] ← heap-size[A] - 1
max_heapify(A,1)
首先,將輸入數組A構造成最大堆,因為數組中最大元素在根A[1],則交換A[1]和A[n]來達到最終正確的位置,此時數組元素最大值為A[n]。現在將A[n]從數組中去掉,可以很容易將A[1..n-1]構造成最大堆。原來的根的子女仍是最大堆,但新的根元素可能違反了最大堆性質,這是調用max_heapify(A,1)就可以保持最大堆性質,在A[1..n-1]中構造最大堆。不斷重復這個過程,直到堆的大小降到2。
下面給出具體C語言實現代碼:
1 void swap(int *a,int *b)
2 {
3 int temp = *a;
4 *a = *b;
5 *b = temp;
6 }
7
8 void max_heapify(int *arr,int i,int size)
9 {
10 int lt = 2*i+1; //左孩子
11 int rt = 2*i+2; //右孩子
12 int large;
13
14 if(lt<=size-1&&arr[lt]>arr[i])
15 large = lt;
16 else
17 large = i;
18 if(rt<=size-1&&arr[rt]>arr[large])
19 large = rt;
20
21 if(large!=i)
22 {
23 swap(&arr[i],&arr[large]);
24 max_heapify(arr,large,size);
25 }
26 }
27
28 void build_max_heap(int *arr,int size)
29 {
30 int i;
31 for(i=size/2;i>=0;i--)
32 {
33 max_heapify(arr,i,size);
34 }
35 }
36
37 void heapsort(int *arr,int size)
38 {
39 int i,len;
40 len = size;
41 build_max_heap(arr,size);
42
43 for(i=size;i>=1;i--)
44 {
45 swap(&arr[0],&arr[i-1]);
46 len--;
47 max_heapify(arr,0,len);
48 }
49 }
50
51 int main(void)
52 {
53 int arr[]={4,1,3,2,16,9,10,14,8,7};
54 int len = sizeof(arr)/sizeof(arr[0]);
55 heapsort(arr,len);
56 int i = 0;
57 for(;i<len;i++)
58 {
59 printf("%d ",arr[i]);
60 }
61 return 0;
62 }
end