一,先介紹一些二叉查找樹的概念和性質。
二叉樹執行基本操作的時間與樹的高度成正比。
設x為二叉查找樹中的一個結點。如果y是x的左子樹中的一個結點,則key[y]<=key[x];如果y是x的右子樹的一個結點,則key[y]>=key[x]。
注意這個性質,這個性質表示二叉查找樹的根節點的左子樹中所有結點都小於根結點,所有右子樹的結點都大於根結點。所以根據這個性質,可以用中序訪問二叉查找數來實現從小大到排列。
二叉查找樹的幾個操作:
SEARCH:查找關鍵字等於key的結點
MINIMUM:找出關鍵字最小的結點
MAXIMUM:找出關鍵字最大的結點
SUCCESSOR:找出結點x的後繼y
INSERT:在二叉查找樹中插入結點z
DELETE:在二叉查找樹中刪除結點z
裡面就INSERT和DELETE麻煩一些。
二、下面分別用偽代碼實現上述操作。
中序遍歷
[plain]
inorder-tree-walk(x)
if x != null
then inorder-tree-walk(left[x])
print(x)
inorder-tree-walk(right[x])
查找
[plain]
tree-search(x, k)
if x == null or k = key[x]
then return x;
if k < key[x]
then return tree-search(left[x], k)
else return tree-search(right[x], k)
時間是樹的高度h=logn
while版本,不用遞歸
while x!= null and k != key[x]
do if(k < key[x])
then x = left[x]
else x = right[x]
return x
最小元素的指針(左子樹的左節點)
[plain]
tree-minimum(x)
while left[x] != null
do x = left[x]
return x
後繼
[plain]
tree-successor(x)
1 if right[x] != null //如果x有右子樹,則在右子樹中尋找最小值
2 then return tree-minimum(right[x])
3 y = parent[x]
4 while y !=null and x == right[y] //如果沒有右子樹,則其後繼y,是x的父親結點的第一個右子樹
5 do x == y
6 y == parent[y]
7 return y
根據其後繼的特性,結點x的後繼是具有大於key[x]中的關鍵字最小者的那個結點。
第1~2行,x的右子樹的結點都是大於key[x]的結點,所以如果x有右子樹,則在右子樹中尋找最小值
第3~6行,如果沒有右子樹,則其後繼y,是x的父親結點的第一個右子樹(根據後繼的特性:結點x的後繼是具有大於key[x]中的關鍵字最小者的那個結點。因為x沒有右子樹,所以這時,按中序遍歷的x下一個結點即後繼,應該是這樣一個子樹的根結點y,x的祖先是其左孩子,這樣,y就大於其左子樹所有結點,並且因為x是y的左子樹中最大的結點了)。
插入:
把結點z插入二叉查找數T中,分以下幾步:
1.將key[z]從根結點x開始比較,並用y記錄x的父親結點,直到到達最後一層某一葉節點比較完,此時y指向某一葉節點,x是NULL。
2.如果此時y是NULL,則證明是空樹,於是根結點就是z
3.否則如果key[z]小於key[y],則讓left[y] = z;當key[z]大於或等於key[y],則讓right[y] = z。
具體為代碼如下:
[plain]
tree-insert(T, z)
y = null
x = root[T]
while x != null
do y = x
if(key[x] < key[z])
then x = right[x]
else x = left[x]
parent[z] = y
if(y == null) //樹是空的
then root[T] = z
else if key[z] < key[y]
then left[y] = z
else right[y] = z
刪除:
有三種情況:
1,沒有左子樹和右子樹。這個就是直接刪除z,把z的父親結點parent[z]指向z的子樹設置為NULL。、
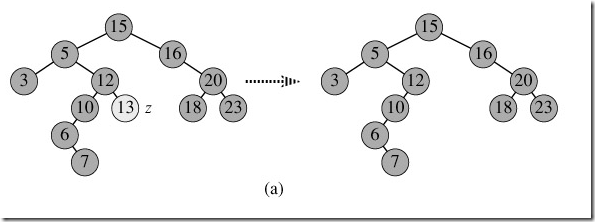
2,只有左子樹或者只有右子樹。這個是讓z的子樹與其父親結點相連,刪除z即可。
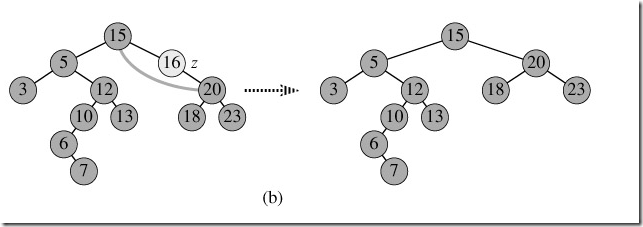
3,既有左子樹又有右子樹。這是先用succeor方法找到要刪除節點z的後繼y,因為y一定沒有左子樹(因為y是z的後繼,參看上文關於後繼的定義,所以y是z的右子樹中最小的一個結點,如果y還有左子樹,則y的左子樹中的結點一定比y小!),所以可以刪除y,並讓y的父親結點成為y的右子樹的父親結點(類似第2中情況),並用y的key代替z的key。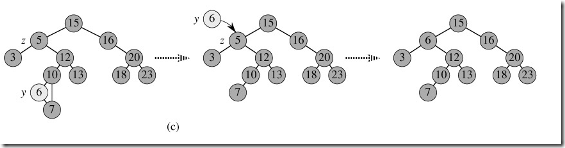

具體偽代碼如下:
[plain]
tree-delete(T, z)
if left[z] == null or right[z] == null //如果沒有做孩子節點或者沒有右孩子節點,及至多有一個子樹
then y = z
else y = tree-successor(z) // 如果都有左孩子和右孩子,則找到他的後繼節點
if left[y] != null
then x = left[y]
else x = right[y]
if x != null // 如果只有一個孩子節點
then parent[x] = parent[y] //讓z的子樹x與其父親結點相連,刪除z即可。
if parent[y] == null //如果y沒有父親節點,說明是根節點
then root[T] = x //則使它的孩子節點為父親節點
else if y == left[parent[y]] //如果y是其父親節點的左子樹,所以可以刪除y,並讓y的父親結點成為y的右子樹的父親結點
then left[parent[y]] = x
else right[parent[y]] = x
if y != z
then key[z] = key[y] //並用y的key代替z的key。
return y