C語言遞歸實現漢諾塔算法

漢諾塔的遞歸實現算法，將A中的圓盤借助B圓盤完全移動到C圓盤上，

每次只能移動一個圓盤，並且每次移動時大盤不能放在小盤上面

遞歸函數的偽算法為如下:

if(n == 1)

直接將A柱子上的圓盤從A移動到C

else

先將A柱子上的n-1個圓盤借助C柱子移動到B柱子上

直接將A柱子上的第n個圓盤移動到C柱子上

最後將B柱子上的n-1個圓盤借助A柱子移動到C柱子上

該遞歸算法的時間復雜度為O（2的n次方)，當有n個圓盤時，需要移動圓盤2的n次方-1次

操作系統：ubuntu

編譯軟件：gcc

結果截圖：

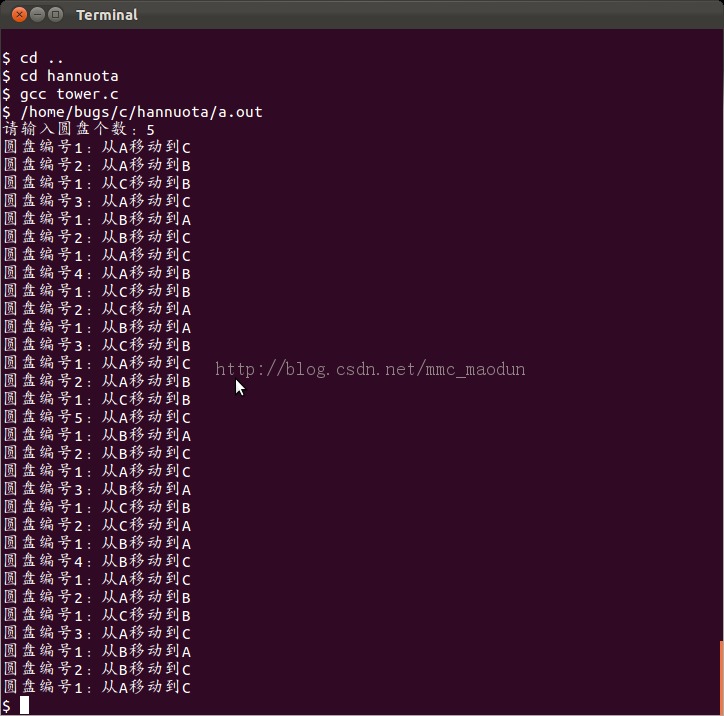
源代碼：

#include<stdio.h>  
      
void move(int,char,char,char);  
      
int main()  
{  
//A、B、C分別代表三個柱子  
char ch1 = 'A';  
char ch2 = 'B';   
char ch3 = 'C';   
      
//n代表圓盤的個數  
int n;  
printf("請輸入圓盤個數：");  
scanf("%d",&n);  
move(n,ch1,ch2,ch3);  
      
return 0;  
}  
      
//將n個圓盤從x柱子借助y柱子移動到z柱子上  
void move(int n,char x,char y,char z)  
{  
if(n == 1)  
  printf("圓盤編號%d：從%c移動到%c\n",n,x,z);  
else
{  
  move(n-1,x,z,y);  
  printf("圓盤編號%d：從%c移動到%c\n",n,x,z);  
  move(n-1,y,x,z);  
}  
}