6.3 二叉樹的遍歷
二叉樹遍歷(Traversal)就是按某種順序對樹中每個結點訪問且只能訪問一次的過程。訪問的含義很廣,如查詢、計算、修改、輸出結點的值。樹遍歷本質上是將非線性結構線性化,它是二叉樹各種運算和操作的實現基礎,需要高度重視。
6.3.1二叉樹的深度優先遍歷
圖6.12二叉樹的遞歸定義 D L R我們是用遞歸的方法來定義二叉樹的。每棵二叉樹由結點、左子樹、右子樹這三個基本部分組成,如果遍歷了這三部分,也就遍歷了整個二叉樹。如圖6.12所示,D為二叉樹中某一結點,L、R分別為結點D的左、右子樹,則其遍歷方式有6種: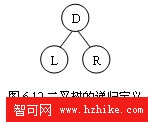
先左後右 先右後左
先序 DLR DRL
中序 LDR RDL
後序 LRD RLD
這裡只討論先左後右的三種遍歷算法。
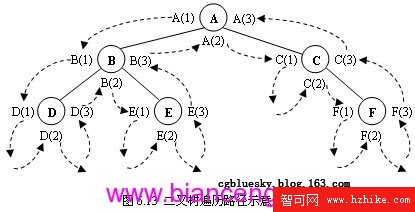
如圖6.13所示,在沿著箭頭方向所指的路徑對二叉樹進行遍歷時,每個節點會在這條搜索路徑上會出現三次,而訪問操作只能進行一次,這時就需要決定在搜索路徑上第幾次出現的結點進行訪問操作,由此就引出了三種不同的遍歷算法。
1.先序遍歷
若二叉樹為非空,則過程為:
(1)訪問根節點。
(2)先序遍歷左子樹。
(3)先序遍歷右子樹。
圖6.13中,先序遍歷就是把標號為(1)的結點按搜索路徑訪問的先後次序連接起來,得出結果為:ABDECF。
2.中序遍歷
若二叉樹為非空,則過程為:
(1)按中序遍歷左子樹。
(2)訪問根結點。
(3)按中序遍歷右子樹。
圖6.13中,先序遍歷就是把標號為(2)的結點按搜索路徑訪問的先後次序連接起來,得出結果為:DBEACF。