C#與數據結構--圖的遍歷(6)

8.3.3 非連通圖的遍歷

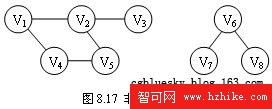
以上討論的圖的兩種遍歷方法都是相對於無向連通圖的，它們都是從一個頂點出發就能訪問到圖中的所有頂點。若無向圖是非連通圖，則只能訪問到初始點所在連通分量中的所有頂點，其他連通分量中的頂點是不可能訪問到的（如圖8.17所示）。為此需要從其他每個連通分量中選擇初始點，分別進行遍歷，才能夠訪問到圖中的所有頂點，否則不能訪問到所有頂點。為此同樣需要再選初始點，繼續進行遍歷，直到圖中的所有頂點都被訪問過為止。

上例的代碼只需對DFSTraverse()方法和BFSTraverse()方法稍作修改，便可以遍歷非連通圖。

public void DFSTraverse() //深度優先遍歷
    {
        InitVisited(); //將visited標志全部置為false
        foreach (Vertex<T> v in items)
        {
            if (!v.visited) //如果未被訪問
            {
                DFS(v); //深度優先遍歷
            }
        }
    }
    public void BFSTraverse() //廣度優先遍歷
    {
        InitVisited(); //將visited標志全部置為false
        foreach (Vertex<T> v in items)
        {
            if (!v.visited) //如果未被訪問
            {
                BFS(v); //廣度優先遍歷
            }
        }