紅黑樹上結點的刪除
紅黑樹本身是一棵二叉查找樹,它的刪除和二叉查找樹的刪除類似。首先要找到真正的刪除點,當被刪除結點n存在左右孩子時,真正的刪除點應該是n的中序遍在前驅,關於這一點請復習二叉查找樹的刪除。如圖9所示,當刪除結點20時,實際被刪除的結點應該為18,結點20的數據變為18。
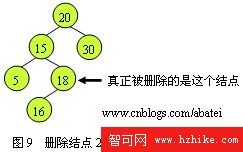
所以可以推斷出,在進行刪除操作時,真正的刪除點必定是只有一個孩子或沒有孩子的結點。而根據紅黑樹的性質可以得出以下兩個結論:
1、刪除操作中真正被刪除的必定是只有一個紅色孩子或沒有孩子的結點。
2、如果真正的刪除點是一個紅色結點,那麼它必定是一個葉子結點。
理解這兩點非常重要,如圖10所示,除了情況(a)外,其他任一種況結點N都無法滿足紅黑樹性質。
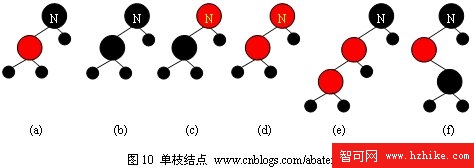
在以下討論中,我們使用藍色箭頭表示真正的刪除點,它也是旋轉操作過程中的第一個判定點;真正的刪除點使用“舊”標注,舊點所在位置將被它的的孩子結點所取代(最多只有一個孩子),我們使用“新”表示舊點的孩子結點。刪除操作可分為以下幾種情形:
1、舊點為紅色結點
若舊點為紅色結點,則它必定是葉子結點,直接刪除即可。如圖11所示
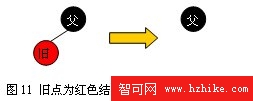
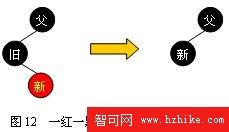
2、一紅一黑
當舊點為黑色結點,新點為紅色結點時,將新點取代舊點位置後,將新點染成紅色即可(如圖12所示)。這裡需要注意:舊點為紅色,新點為黑色的情況不可能存在。