用C#設計與實現一個四則算術運算解釋器(5)

這裡為止，我們可以得出一個很重要的法則：插入一個新的操作符進入 AST 樹的時候，若是樹的根是一個操作符，並且和此新操作符同級，運算順序是由左至右的話，那麼新的操作符會成為新的樹的根，現有的樹會成為新樹的左子樹。

實際上，整個解釋器的開發，遵從“啟發式 heuristic ”的原理。整個解釋的過程可以分解成一條條的“規則”，我們需要做的是把規則全部“找”出來，並且把規則制定的盡可能完善。

好了，回到剛才的分析上。假設要插入的操作符不是 +，而是一個優先權比較高的 * 呢？也就是，若是 1 + 2 * 3 的話，AST 會是什麼樣子？

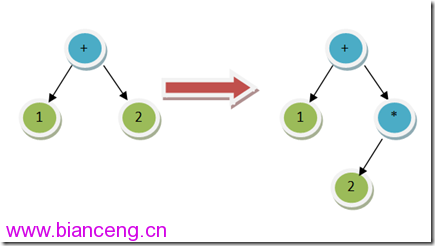
這種情況下，乘法運算符必須移動到樹的右子樹上，並且成為右子樹的根。原右子樹會成為新的右子樹的左子樹。

插入操作符的代碼實現如下：

if　(token　is　OpToken)　{

　　if　(root.Token　is　OpToken　&&　root.RightChild　==　null)　{

　　　　throw　new　ParseFailureException(
　　　　　　"The　expression　'{0}　{1}'　is　not　a　valid　arithmetic　expression.",
　　　　　　root.Token.ToString(),
　　　　　　token.ToString()
　　　　);

　　}

　　if　(root.Token　is　NumToken)　{

　　　　Syntax　newRoot　=　new　Syntax(token);
　　　　newRoot.LeftChild　=　root;
　　　　root　=　newRoot;

　　　　return　newRoot;

　　}

　　if　(root.Token　is　OpToken)　{

　　　　//　Compare　prioirty　of　the　two　Operators
　　　　OpToken　token1　=　(OpToken)token;
　　　　OpToken　token2　=　(OpToken)root.Token;

　　　　if　(token1.Prioirty　<=　token2.Prioirty)　{

　　　　　　Syntax　newRoot　=　new　Syntax(token1);
　　　　　　newRoot.LeftChild　=　root;
　　　　　　root　=　newRoot;

　　　　　　return　newRoot;

　　　　}

　　　　if　(token1.Prioirty　>　token2.Prioirty)　{

　　　　　　root.RightChild　=　Append(root.RightChild,　token);

　　　　　　return　root;
　　　　}
　　}
}