從例子可以看出,在未賦值之前,n的值為空,和其他值運算不會發生錯誤。下面是語法樹分析的圖:
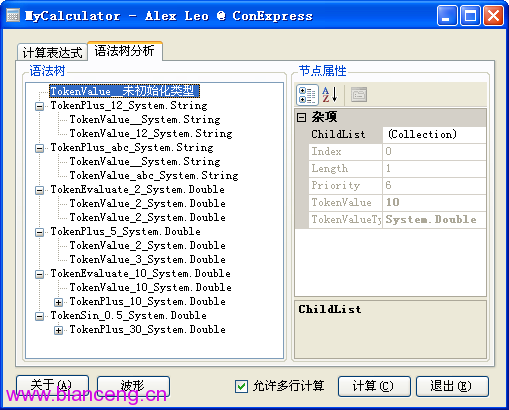
從圖上可以看出變量n是引用的,在第一句中n的值是空,類型為未初始化類型,但是在PropertyGrid中顯示的信息是最後一次賦值的結果。 而且這裡把賦值操作符"="作為賦值操作的根節點,並沒有像左括號"("一樣處理。比如最後一個表達式sin(n+20)的語法 樹中,TokenSin的下級是TokenPlus,而不是TokenLeftBracket。對於賦值操作符"="之所以這保留了原始結構,是因為這樣可以在 修改下級節點的值之後繼續調用Execute方法進行計算,否則如果把值直接指定給變量,下次調用Execute的時候就沒法執行了。左括號只是分 割表達式,但賦值操作符是有真正的運算過程,所以必須用不一樣的分析方法。這一點對於下面要實現的函數波形非常重要。在繪制波形的時 候需要改變變量,如果采用變量字符串替換的方法,每次都需要分析表達式,而變量的值域可能很大,這樣會把大量時間消耗在分析上。但是 如果能保留完整的語法樹,只需要將變量對應的TokenRecord的值改變,再次調用頂級節點的Execute方法,這時候只需要逐級向下調用計算方 法即可,不需要重新分析表達式了。
接下來就介紹怎麼實現函數波形繪制的吧。首先這裡引入了一個變量n,在進行計算之前在程序裡面進行初始化,然後根據設置的范圍用for 遞增。定義兩個表達式X和Y,分別對應坐標點的X和Y,這兩個表達式中包含n,在對n進行遞增之前調用語法分析類進行分析,得到頂級節點, 這時候語法樹已經分析完成了。在對n進行遞增的時候,計算X和Y,形成一系列坐標點。調用Graphics類的DrawLines方法,把計算得到的一系 列坐標點作為參數傳遞給該方法,這樣就可以看到特定的波形。
比如阿基米德螺旋線用偽代碼表示如下:
for(int n = 1; n < 360; n++)
{
X = n*sin(n);
Y = n*cos(n);
PointCollection.Add(new Point(X, Y));
}
myGraphics.DrawLines(myPen, PointCollection);
在本程序裡阿基米德螺旋線的偽代碼可以表示如下:
strN = "n=0";
strX = "n*sin(n)";
strY = "n*cos(n)";
TokenN = mySyntaxAnalyse.Analyse(strN);
TokenX = mySyntaxAnalyse.Analyse(strX);
TokenY = mySyntaxAnalyse.Analyse(strY);
for(int index = 1; n < 360; n++)
{
TokenN.TokenValue = index;
TokenX.Execute();
TokenY.Execute();
PointCollection.Add(new Point(TokenX.TokenValue, TokenY.TokenValue));
}
myGraphics.DrawLines(myPen, PointCollection);