摘要:
本文介紹了一種國際上通用的加密算法—DES算法的原理,並給出了在VC++6.0語言環境下實現的源代碼。最後給出一個示例,以供參考。
關鍵字:DES算法、明文、密文、密鑰、VC;
本文程序運行效果圖如下:

正文:
當今社會是信息化的社會。為了適應社會對計算機數據安全保密越來越高的要求,美國國家標准局(NBS)於1997年公布了一個由IBM公司研制的一種加密算法,並且確定為非機要部門使用的數據加密標准,簡稱DES(Data Encrypton Standard)。自公布之日起,DES算法作為國際上商用保密通信和計算機通信的最常用算法,一直活躍在國際保密通信的舞台上,扮演了十分突出的角色。現將DES算法簡單介紹一下,並給出實現DES算法的VC源代碼。
DES算法由加密、解密和子密鑰的生成三部分組成。
一.加密
DES算法處理的數據對象是一組64比特的明文串。設該明文串為m=m1m2…m64 (mi=0或1)。明文串經過64比特的密鑰K來加密,最後生成長度為64比特的密文E。其加密過程圖示如下:
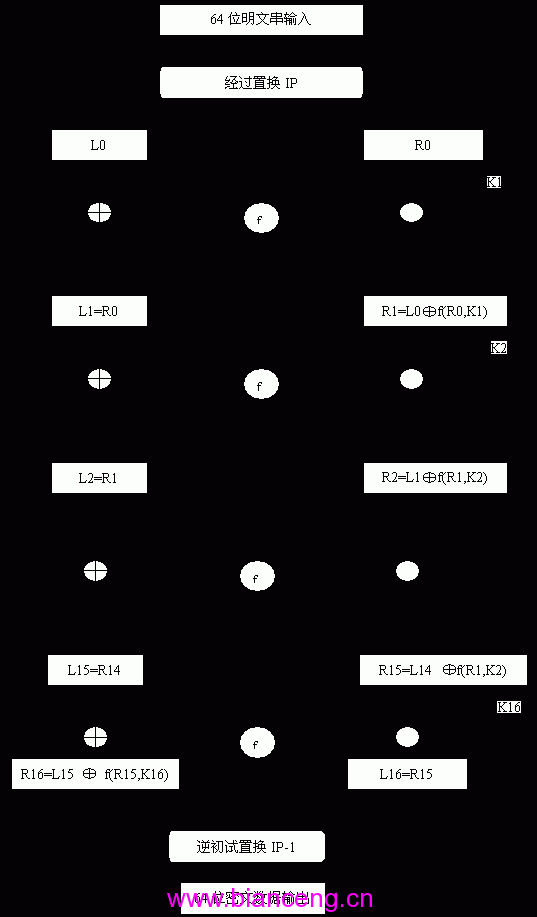
DES算法加密過程
對DES算法加密過程圖示的說明如下:待加密的64比特明文串m,經過IP置換後,得到的比特串的下標列表如下:
IP 58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4 62 54 46 38 30 22 14 6 64 56 48 40 32 24 16 8 57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3 61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7
該比特串被分為32位的L0和32位的R0兩部分。R0子密鑰K1(子密鑰的生成將在後面講)經過變換f(R0,K1)(f變換將在下面講)輸出32位的比特串f1,f1與L0做不進位的二進制加法運算。運算規則為:
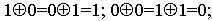
f1與L0做不進位的二進制加法運算後的結果賦給R1,R0則原封不動的賦給L1。L1與R0又做與以上完全相同的運算,生成L2,R2…… 一共經過16次運算。最後生成R16和L16。其中R16為L15與f(R15,K16)做不進位二進制加法運算的結果,L16是R15的直接賦值。
R16與L16合並成64位的比特串。值得注意的是R16一定要排在L16前面。R16與L16合並後成的比特串,經過置換IP-1後所得比特串的下標列表如下:
IP-1 40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31 38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29 36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 26 33 1 41 9 49 17 57 25
經過置換IP-1後生成的比特串就是密文e.。
下面再講一下變換f(Ri-1,Ki)。
它的功能是將32比特的輸入再轉化為32比特的輸出。其過程如圖所示:
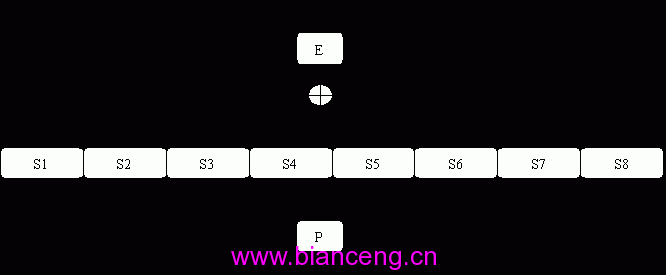
對f變換說明如下:輸入Ri-1(32比特)經過變換E後,膨脹為48比特。膨脹後的比特串的下標列表如下:
E: 32 1 2 3 4 5 4 5 6 7 8 9 8 9 10 11 12 13 12 13 14 15 16 17 16 17 18 19 20 21 20 21 22 23 24 25 24 25 26 27 28 29 28 29 30 31 32 31
膨脹後的比特串分為8組,每組6比特。各組經過各自的S盒後,又變為4比特(具體過程見後),合並後又成為32比特。該32比特經過P變換後,其下標列表如下:
P: 16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25
經過P變換後輸出的比特串才是32比特的f (Ri-1,Ki)。
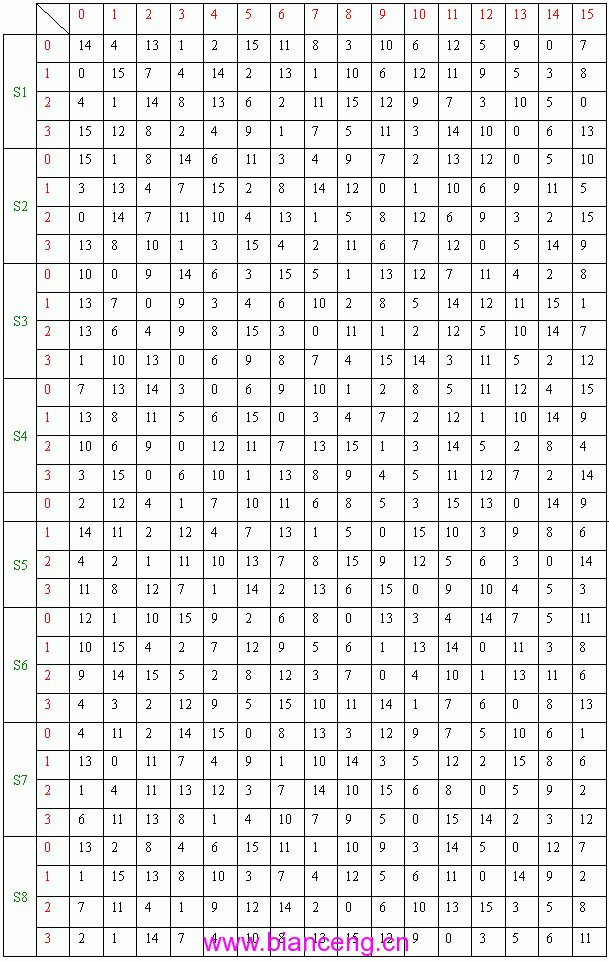
下面再講一下S盒的變換過程。任取一S盒。見圖:
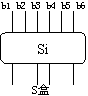
在其輸入b1,b2,b3,b4,b5,b6中,計算出x=b1*2+b6, y=b5+b4*2+b3*4+b2*8,再從Si表中查出x 行,y 列的值Sxy。將Sxy化為二進制,即得Si盒的輸出。(S表如圖所示)
至此,DES算法加密原理講完了。在VC++6.0下的程序源代碼為:
for(i=1;i<=64;i++)下面進行迭代。由於各次迭代的方法相同只是輸入輸出不同,因此只給出其中一次。以第八次為例:
m1[i]=m[ip[i-1]];//64位明文串輸入,經過IP置換。//進行第八次迭代。首先進行S盒的運算,輸入32位比特串。
for(i=1;i<=48;i++)//經過E變換擴充,由32位變為48位
RE1[i]=R7[E[i-1]];
for(i=1;i<=48;i++)//與K8按位作不進位加法運算
RE1[i]=RE1[i]+K8[i];
for(i=1;i<=48;i++)
{
if(RE1[i]==2)
RE1[i]=0;
}
for(i=1;i<7;i++)//48位分成8組
{
s11[i]=RE1[i];
s21[i]=RE1[i+6];
s31[i]=RE1[i+12];
s41[i]=RE1[i+18];
s51[i]=RE1[i+24];
s61[i]=RE1[i+30];
s71[i]=RE1[i+36];
s81[i]=RE1[i+42];
}//下面經過S盒,得到8個數。S1,s2,s3,s4,s5,s6,s7,s8分別為S表
s[1]=s1[s11[6]+s11[1]*2][s11[5]+s11[4]*2+s11[3]*4+s11[2]*8];
s[2]=s2[s21[6]+s21[1]*2][s21[5]+s21[4]*2+s21[3]*4+s21[2]*8];
s[3]=s3[s31[6]+s31[1]*2][s31[5]+s31[4]*2+s31[3]*4+s31[2]*8];
s[4]=s4[s41[6]+s41[1]*2][s41[5]+s41[4]*2+s41[3]*4+s41[2]*8];
s[5]=s5[s51[6]+s51[1]*2][s51[5]+s51[4]*2+s51[3]*4+s51[2]*8];
s[6]=s6[s61[6]+s61[1]*2][s61[5]+s61[4]*2+s61[3]*4+s61[2]*8];
s[7]=s7[s71[6]+s71[1]*2][s71[5]+s71[4]*2+s71[3]*4+s71[2]*8];
s[8]=s8[s81[6]+s81[1]*2][s81[5]+s81[4]*2+s81[3]*4+s81[2]*8];
for(i=0;i<8;i++)//8個數變換輸出二進制
{
for(j=1;j<5;j++)
{
temp[j]=s[i+1]%2;
s[i+1]=s[i+1]/2;
}
for(j=1;j<5;j++)
f[4*i+j]=temp[5-j];
}
for(i=1;i<33;i++)//經過P變換
frk[i]=f[P[i-1]];//S盒運算完成
for(i=1;i<33;i++)//左右交換
L8[i]=R7[i];
for(i=1;i<33;i++)//R8為L7與f(R,K)進行不進位二進制加法運算結果
{
R8[i]=L7[i]+frk[i];
if(R8[i]==2)
R8[i]=0;
}
其它各次迭代類似,可以依此類推。
本文配套源碼