任意點集的三角網格化(triangulation)問題一直是人們密切關注的問題。三角網格化問題在許多領域有廣泛應用。Delaunay 三角剖分是目前研究應用最廣的一種剖分方法,因其具備很多優點,以下簡單列舉兩條:
空外接圓性質:在由點集V-生成的D-三角網中,每個三角形的外接圓均不包含該點集的其他任意點。
最大最小角度性質:在由點集V-生成的D-三角網中,所有三角形中的最小角度是最大的。
Open CV中有Delaunay的實現,極大地方便了廣大科研工作者。盡管Open CV提供了詳細的文檔,並且提供了相關sample,但是由於對原文檔及參考書籍[1,3,4]的理解上的不足,筆者在使用過程中仍然遇到很多問題,下面將自己的一些理解及探索進行總結,謬誤之處望大家批評指正。請注意,這裡並不會詳細介紹Open CV如何進行delaunay劃分,請參考Open CV自帶的示例程序delaunay.c.
1.也說“四方邊緣(Quad-edge)”結構
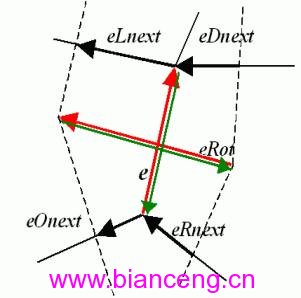
圖1 邊e以及與邊e相關的邊(該圖來自Open CV文檔)
這個結構圖非常難懂(對我而言),但是非常關鍵,是Open CV 平面劃分的最基本元素,數據結構如下:
/* quad-edge structure fields */
#define CV_QUADEDGE2D_FIELDS() \
int flags; \
struct CvSubdiv2DPoint* pt[4]; \
CvSubdiv2DEdge next[4];
typedef struct CvQuadEdge2D
{
CV_QUADEDGE2D_FIELDS()
}
CvQuadEdge2D;
這個結構的關鍵數據是數組next[4],其按順序存放四條邊(代碼):e,eRot以及它們的反向邊。注:我這裡用“邊代碼”,原因是Open CV是用long型的代碼來表示平面劃分的一條邊。
eLnext: e的左方區域(或上方區域)是一個多邊形,e是其中一條邊,eLnext是指向這個區域的另一條邊,這個描述有點類似於數據結構中的十字鏈表的表示法,與e是連接在一起的;
eRnext: 理解同eLnext,只不過是指向e的右方區域(或下方區域)的另一條邊,與e是連接在一起的;
eDnext: 與e共“目的點”的另一條邊;
eOnext: 與e共“出發點”的另一條邊;
eRot: e的對偶邊,這就沒什麼好解釋的了。
在了解這些知識點後,我們可以獲得如下的應用:
2.應用1-在Delaunay劃分結束後獲取三角形連接關系
(1) 首先,以邊e開始循環查找與其相連的兩條邊就可以找到一個三角形,對所有邊進行相同操作,就可以找到許多三角形,注意,這其中有許多重復的邊,需要進行判斷。主要代碼如下:
for( i = 0; i < total; i++ ) // total是邊數目,可以參考Open CV示例程序delaunay.c
{
CvQuadEdge2D* edge = (CvQuadEdge2D*)(reader.ptr);
if( CV_IS_SET_ELEM( edge ))
{
CvSubdiv2DEdge e = (CvSubdiv2DEdge)edge;
CvSubdiv2DEdge t = e;
CvPoint buf[3];
int iPointNum = 3;
for(int j = 0; j < iPointNum; j++ ){
CvSubdiv2DPoint* pt = cvSubdiv2DEdgeOrg( t );
if( !pt ) break;
buf[j] = cvPoint( cvRound(pt->pt.x), cvRound(pt->pt.y));
t = cvSubdiv2DGetEdge( t, CV_NEXT_AROUND_LEFT );
}
if (j == iPointNum) {
AddTriangle(buf); // 添加三角形
}
CV_NEXT_SEQ_ELEM( elem_size, reader );
}
(2) 其次,因為在Delaunay劃分中,所有邊是有方向的,光通過e進行輪循可能會遺失部分三角形,因此同時還得以e的反向邊進行輪循,上面的代碼可以改為如下:Bool FindTriangleFromEdge(CvSubdiv2DEdge e)
{
CvSubdiv2DEdge t = e;
CvPoint buf[3];
CvPoint *pBuf = buf;
int iPointNum = 3;
for(int j = 0; j < iPointNum; j++ ){
CvSubdiv2DPoint* pt = cvSubdiv2DEdgeOrg( t );
if( !pt ) break;
buf[j] = cvPoint( cvRound(pt->pt.x), cvRound(pt->pt.y));
t = cvSubdiv2DGetEdge( t, CV_NEXT_AROUND_LEFT );
}
if (j == iPointNum) {
AddTriangle(buf); // 添加三角形
return true;
}
return false;
}
// 調用代碼如下
for( i = 0; i < total; i++ )
{
CvQuadEdge2D* edge = (CvQuadEdge2D*)(reader.ptr);
if( CV_IS_SET_ELEM( edge ))
{
CvSubdiv2DEdge e = (CvSubdiv2DEdge)edge;
FindTriangleFromEdge(e);
CvSubdiv2DEdge e1 = (CvSubdiv2DEdge)edge+2; //即next[2]
FindTriangleFromEdge(e1);
}
CV_NEXT_SEQ_ELEM( elem_size, reader );
}
在上面的代碼中,是直接采用數組位移法進行各種邊的對應的(即edge+2),不過Open CV已經有了自己的實現函數:cvSubdiv2DRotateEdge,上面用紅色粗體標注的語句可以換為:CvSubdiv2DEdge e1 = cvSubdiv2DRotateEdge((CvSubdiv2DEdge)edge,2);
對於16個點的輸入,Delaunay分割的結果如圖2所示。
3. 應用2-在Vonoroi劃分結束後獲取多邊形
參考Delaunay.c中的函數:void paint_voronoi( CvSubdiv2D* subdiv, IplImage* img );結果如圖3所示。
有了應用1的分析,理解這段代碼也很容易。
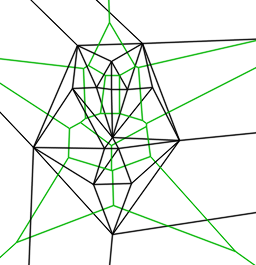
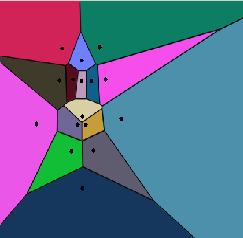 圖2. 16個點的Delaunay三角剖分結果
圖3. 相應的Voronoi劃分結果
圖2. 16個點的Delaunay三角剖分結果
圖3. 相應的Voronoi劃分結果
注:讀者要編譯附帶源程序,請安裝Open CV庫1.0正式版(最好安裝在默認目錄,否則需要修改工程配置路徑)。
本文配套源碼