漢諾塔問題是最經典的遞歸問題,筆者就該問題設計了這個游戲,由用戶交互 游戲和自動演示兩部分組成,支持撤銷功能、選關、自動完成等功能。
首先 建立了類CMap,該類主要實現用戶每一步的操作和畫圖顯示功能,記錄的時候只 須記錄每組盤子的個數和盤子的矩形。代碼和注釋如下:
//記錄 每一步的盤子的情況
class CMap
{
public:
//每組 盤子的個數
int iCount[3];
//3組盤子裡面,每個盤子的位 置,用矩形表示
RECT *Rect[3];
//構造函數
CMap()
{
//三組盤子,每組盤子的矩形
for(int i=0;i<3;i++)
Rect[i]=new RECT[NUM];
//初始化每組盤子的個數
iCount[0]=NUM;
iCount[1]=0;
iCount[2]=0;
//第一組盤子的矩形 的位置
for(i=0;i<NUM;i++)
{
Rect[0][i].left=Center[0]-(NUM-i)*Dx2;
Rect[0] [i].right=Center[0]+(NUM-i)*Dx2;
Rect[0][i].bottom= (NUM+1-i)*Dx;
Rect[0][i].top=(NUM-i)*Dx;
}
//第二組盤子的矩形初始化為空
for (i=0;i<NUM;i++)
{
Rect[1] [i].left=0;
Rect[1][i].right=0;
Rect [1][i].bottom=0;
Rect[1][i].top=0;
}
//第三組盤子的矩形初始化為空
for (i=0;i<NUM;i++)
{
Rect[2] [i].left=0;
Rect[2][i].right=0;
Rect [2][i].bottom=0;
Rect[2][i].top=0;
}
}
//運算符重載
CMap operator=(CMap Other)
{
//對新的CMap對象,應該重新分配內存
for (int i=0;i<3;i++)
Rect[i]=new RECT[NUM];
//依次賦值
for(i=0;i<3;i++)
{
iCount[i]=Other.iCount[i];
for(int j=0;j<NUM;j++)
Rect[i][j]=Other.Rect[i][j];
}
//返回
return *(this);
}
//畫圖,顯示盤子的情況
void OnDraw(HDC hdc)
{
//畫出每個盤子
for(int i=0;i<3;i++)
for(int j=0;j<iCount[i];j++)
Rectangle(hdc,
Rect[i][j].left,
Rect[i][j].top,
Rect[i] [j].right,
Rect[i][j].bottom);
}
//析構函數
~CMap()
{
//內存的釋放
for(int i=0;i<3;i++)
{
if(Rect[i]!=NULL)
{
Rect[i] =NULL;
delete Rect[i];
}
}
}
};
下面是漢諾塔的主類Hanio,該類的成員函 數有OnDraw(),Undo(),Move(),AutoMove()等,分別實現漢諾塔的畫圖顯示、 撤銷、移動盤子、自動移動盤子等功能,代碼及注釋如下:class Hanio
{
public:
//當前的步數
int iStep;
//記錄每一步的盤子的情況
CMap Record[MAXSTEP];
public:
//構造函數
Hanio()
{
//初始化,步數為0
iStep=0;
//初始化記錄
for(int i=0;i<MAXSTEP;i++)
{
Record[i]=CMap();
}
}
//畫圖,顯示漢諾塔 的情況
void OnDraw(HDC hdc)
{
Record [iStep].OnDraw(hdc);
}
//撤銷
void Undo()
{
if(iStep>0)
iStep--;
//重繪
Draw();
}
//移動盤子
void Move(int iStart,int iEnd)
{
//得到當前盤子 的記錄
CMap Map=Record[iStep];
//移動的情況判 斷,去除非法的移動
if(iStart<0||iStart>=3)
return;
if(iEnd<0||iEnd>=3)
return;
if(iStart==iEnd)
return;
if(Map.iCount[iStart]<1)
return;
//得到移動前的開始組,結束組的盤子的個數
int iStartRectNum=Map.iCount[iStart];
int iEndRectNum=Map.iCount[iEnd];
//從小盤子移動到大盤子上面的 情況是不可以的。
if(iEndRectNum>0)
if (Width(Map.Rect[iStart][iStartRectNum-1])>=Width(Map.Rect[iEnd] [iEndRectNum-1]))
return;
//步數累加
iStep++;
//記錄新的盤子的情況
Record[iStep]=Record[iStep-1];
//移走的那一組盤子的個數減 少
Record[iStep].iCount[iStart]--;
//被移到的 那一組的盤子個數增加
Record[iStep].iCount[iEnd]++;
//重新計算移動後的盤子的矩形
//主要是被移到的那一組 的最上面那個盤子的矩形的計算
RECT rect;
rect.left=Center[iEnd]-Width(Map.Rect[iStart][iStartRectNum-1])/2;
rect.right=Center[iEnd]+Width(Map.Rect[iStart][iStartRectNum -1])/2;
rect.bottom=(NUM+1-Map.iCount[iEnd])*Dx;
rect.top=(NUM-Map.iCount[iEnd])*Dx;
Record [iStep].Rect[iEnd][iEndRectNum]=rect;
//刷新
SendMessage(hWnd,WM_PAINT,0,0);
}
//自動移盤子
void AutoMove(int iA,int iB,int iC,int iNum)
{
//遞歸實現自動移盤子
//遞歸的出口,如果個數為3,按如下進 行移動。
if(iNum==3)
{
Move (iA,iC);
::Sleep(500);
Move (iA,iB);
::Sleep(500);
Move (iC,iB);
::Sleep(500);
Move (iA,iC);
::Sleep(500);
Move (iB,iA);
::Sleep(500);
Move (iB,iC);
::Sleep(500);
Move (iA,iC);
::Sleep(500);
}
// 個數大於3,遞歸實現移動。
else
{
//遞歸自動移動。
AutoMove(iA,iC,iB,iNum-1);
Move(iA,iC);
::Sleep(500);
AutoMove(iB,iA,iC,iNum-1);
}
}
};
程序實現的結果如下圖:
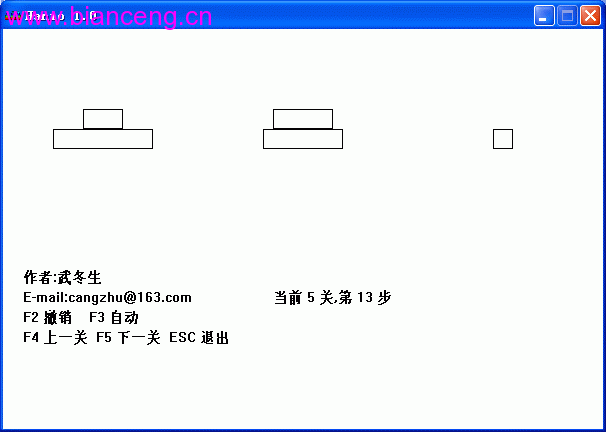
由於堆棧內存的限制,選關不可能是無限個盤子,本程序設計的最大關數是8。自 動移動是用遞歸實現的,自動移動的過程中,其他消息無法響應,可以改成多線 程或由用戶控制的形式。上述的程序附有Visual C++源代碼,並在Windows XP和 Visual C++6.0下調試成功。
本文配套源碼