OpenGL通過相機模擬、可以實現計算機圖形學中最基本的三維變換,即幾何變換、投影變換、裁剪變換、視口變換等,同時,OpenGL還實現了矩陣堆棧等。理解掌握了有關坐標變換的內容,就算真正走進了精彩地三維世界。
一、OpenGL中的三維物體的顯示
(一)坐標系統
在現實世界中,所有的物體都具有三維特征,但計算機本身只能處理數字,顯示二維的圖形,將三維物體及二維數據聯系在一起的唯一紐帶就是坐標。
為了使被顯示的三維物體數字化,要在被顯示的物體所在的空間中定義一個坐標系。這個坐標系的長度單位和坐標軸的方向要適合對被顯示物體的描述,這個坐標系稱為世界坐標系。世界坐標系是始終固定不變的。
OpenGL還定義了局部坐標系的概念,所謂局部坐標系,也就是坐標系以物體的中心為坐標原點,物體的旋轉或平移等操作都是圍繞局部坐標系進行的,這時,當物體模型進行旋轉或平移等操作時,局部坐標系也執行相應的旋轉或平移操作。需要注意的是,如果對物體模型進行縮放操作,則局部坐標系也要進行相應的縮放,如果縮放比例在案各坐標軸上不同,那麼再經過旋轉操作後,局部坐標軸之間可能不再相互垂直。無論是在世界坐標系中進行轉換還是在局部坐標系中進行轉換,程序代碼是相同的,只是不同的坐標系考慮的轉換方式不同罷了。
計算機對數字化的顯示物體作了加工處理後,要在圖形顯示器上顯示,這就要在圖形顯示器屏幕上定義一個二維直角坐標系,這個坐標系稱為屏幕坐標系。這個坐標系坐標軸的方向通常取成平行於屏幕的邊緣,坐標原點取在左下角,長度單位常取成一個象素。
(二)三維物體的相機模擬
為了說明在三維物體到二維圖象之間,需要經過什麼樣的變換,我們引入了相機(Camera)模擬的方式,假定用相機來拍攝這個世界,那麼在相機的取景器中,就存在人眼和現實世界之間的一個變換過程。
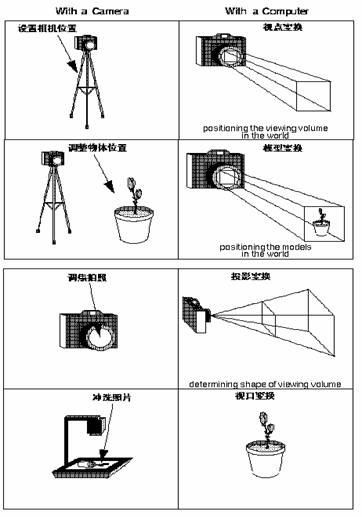
圖一、相機模擬OpenGL中的各種坐標變換
從三維物體到二維圖象,就如同用相機拍照一樣,通常都要經歷以下幾個步驟:
1、將相機置於三角架上,讓它對准三維景物,它相當於OpenGL中調整視點的位置,即視點變換(Viewing Transformation)。
2、將三維物體放在場景中的適當位置,它相當於OpenGL中的模型變換(Modeling Transformation),即對模型進行旋轉、平移和縮放。
3、選擇相機鏡頭並調焦,使三維物體投影在二維膠片上,它相當於OpenGL中把三維模型投影到二維屏幕上的過程,即OpenGL的投影變換(Projection Transformation),OpenGL中投影的方法有兩種,即正射投影和透視投影。為了使顯示的物體能以合適的位置、大小和方向顯示出來,必須要通過投影。有時為了突出圖形的一部分,只把圖形的某一部分顯示出來,這時可以定義一個三維視景體(Viewing Volume)。正射投影時一般是一個長方體的視景體,透視投影時一般是一個稜台似的視景體。只有視景體內的物體能被投影在顯示平面上,其他部分則不能。
4、沖洗底片,決定二維相片的大小,它相當與OpenGL中的視口變換(Viewport Transformation)(在屏幕窗口內可以定義一個矩形,稱為視口(Viewport),視景體投影後的圖形就在視口內顯示)規定屏幕上顯示場景的范圍和尺寸。
通過上面的幾個步驟,一個三維空間裡的物體就可以用相應的二維平面物體表示了,也就能在二維的電腦屏幕上正確顯示了。總的來說,三維物體的顯示過程如下:
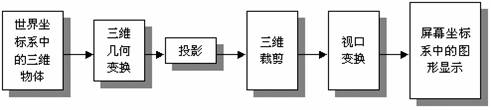
圖二、三維物體的顯示過程
二、OpenGL中的幾種變換
OpenGL中的各種轉換是通過矩陣運算實現的,具體的說,就是當發出一個轉換命令時,該命令會生成一個4X4階的轉換矩陣(OpenGL中的物體坐標一律采用齊次坐標,即(x, y, z, w),故所有變換矩陣都采用4X4矩陣),當前矩陣與這個轉換矩陣相乘,從而生成新的當前矩陣。例如,對於頂點坐標v ,轉換命令通常在頂點坐標命令之前發出,若當前矩陣為C,轉換命令構成的矩陣為M,則發出轉換命令後,生成的新的當前矩陣為CM,這個矩陣再乘以頂點坐標v,從而構成新的頂點坐標CMv。上述過程說明,程序中繪制頂點前的最後一個變換命令最先作用於頂點之上。這同時也說明,OpenGL編程中,實際的變換順序與指定的順序是相反的。
(一)視點變換
視點變換確定了場景中物體的視點位置和方向,就向上邊提到的,它象是在場景中放置了一架照相機,讓相機對准要拍攝的物體。確省時,相機(即視點)定位在坐標系的原點(相機初始方向都指向Z負軸),它同物體模型的缺省位置是一致的,顯然,如果不進行視點變換,相機和物體是重疊在一起的。
執行視點變換的命令和執行模型轉換的命令是相同的,想一想,在用相機拍攝物體時,我們可以保持物體的位置不動,而將相機移離物體,這就相當於視點變換;另外,我們也可以保持相機的固定位置,將物體移離相機,這就相當於模型轉換。這樣,在OpenGL中,以逆時針旋轉物體就相當於以順時針旋轉相機。因此,我們必須把視點轉換和模型轉換結合在一起考慮,而對這兩種轉換單獨進行考慮是毫無意義的。
除了用模型轉換命令執行視點轉換之外,OpenGL實用庫還提供了gluLookAt()函數,該函數有三個變量,分別定義了視點的位置、相機瞄准方向的參考點以及相機的向上方向。該函數的原型為:
void gluLookAt(GLdouble eyex,GLdouble eyey,GLdouble eyez,GLdouble centerx,GLdouble centery,GLdouble upx,GLdouble upy,GLdouble upz);
該函數定義了視點矩陣,並用該矩陣乘以當前矩陣。eyex,eyey,eyez定義了視點的位置;centerx、centery和centerz變量指定了參考點的位置,該點通常為相機所瞄准的場景中心軸線上的點;upx、upy、upz變量指定了向上向量的方向。
通常,視點轉換操作在模型轉換操作之前發出,以便模型轉換先對物體發生作用。場景中物體的頂點經過模型轉換之後移動到所希望的位置,然後再對場景進行視點定位等操作。模型轉換和視點轉換共同構成模型視景矩陣。
(二)模型變換
模型變換是在世界坐標系中進行的。缺省時,物體模型的中心定位在坐標系的中心處。OpenGL在這個坐標系中,有三個命令,可以模型變換。
1、模型平移
glTranslate{fd}(TYPE x,TYPE y,TYPE z);
該函數用指定的x,y,z值沿著x軸、y軸、z軸平移物體(或按照相同的量值移動局部坐標系)。
2、模型旋轉
glRotate{fd}(TYPE angle,TYPE x,TYPE,y,TYPE z);
該函數中第一個變量angle制定模型旋轉的角度,單位為度,後三個變量表示以原點(0,0,0)到點(x,y,z)的連線為軸線逆時針旋轉物體。例如,glRotatef(45.0,0.0,0.0,1.0)的結果是繞z軸旋轉45度。
3、模型縮放
glScale{fd}(TYPE x,TYPE y,TYPE z);
該函數可以對物體沿著x,y,z軸分別進行放大縮小。函數中的三個參數分別是x、y、z軸方向的比例變換因子。缺省時都為1.0,即物體沒變化。程序中物體Y軸比例為2.0,其余都為1.0,就是說將立方體變成長方體。
(三)投影變換
經過模型視景的轉換後,場景中的物體放在了所希望的位置上,但由於顯示器只能用二維圖象顯示三維物體,因此就要靠投影來降低維數(投影變換類似於選擇相機的鏡頭)。
事實上,投影變換的目的就是定義一個視景體,使得視景體外多余的部分裁剪掉,最終進入圖像的只是視景體內的有關部分。投影包括透視投影(Perspective Projection)和正視投影(Orthographic Projection)兩種。
透視投影,符合人們心理習慣,即離視點近的物體大,離視點遠的物體小,遠到極點即為消失,成為滅點。它的視景體類似於一個頂部和底部都被進行切割過的稜椎,也就是稜台。這個投影通常用於動畫、視覺仿真以及其它許多具有真實性反映的方面。
OpenGL透視投影函數有兩個,其中函數glFrustum()的原型為:
void glFrustum(GLdouble left,GLdouble Right,GLdouble bottom,GLdouble top,GLdouble near,GLdouble far);
它創建一個透視視景體。其操作是創建一個透視投影矩陣,並且用這個矩陣乘以當前矩陣。這個函數的參數只定義近裁剪平面的左下角點和右上角點的三維空間坐標,即(left,bottom,-near)和(right,top,-near);最後一個參數far是遠裁剪平面的Z負值,其左下角點和右上角點空間坐標由函數根據透視投影原理自動生成。near和far表示離視點的遠近,它們總為正值。該函數形成的視景體如圖三所示。
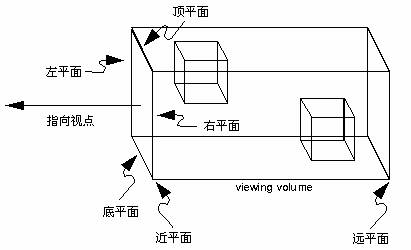
圖三、透視投影視景體
另一個透視函數是:
void gluPerspective(GLdouble fovy,GLdouble aspect,GLdouble zNear, GLdouble zFar);
它也創建一個對稱透視視景體,但它的參數定義於前面的不同,參數fovy定義視野在X-Z平面的角度,范圍是[0.0, 180.0];參數aspect是投影平面寬度與高度的比率;參數zNear和Far分別是遠近裁剪面沿Z負軸到視點的距離,它們總為正值。
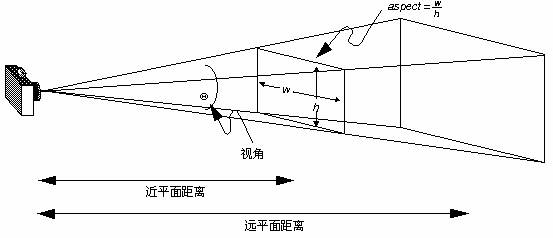
圖四、透視投影視景體
以上兩個函數缺省時,視點都在原點,視線沿Z軸指向負方向。
正射投影,又叫平行投影。這種投影的視景體是一個矩形的平行管道,也就是一個長方體,如圖五所示。正射投影的最大一個特點是無論物體距離相機多遠,投影後的物體大小尺寸不變。這種投影通常用在建築藍圖繪制和計算機輔助設計等方面,這些行業要求投影後的物體尺寸及相互間的角度不變,以便施工或制造時物體比例大小正確。

圖五、正射投影視景體
OpenGL正射投影函數也有兩個,一個函數是:
void glOrtho(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top, GLdouble near,GLdouble far)
它創建一個平行視景體。實際上這個函數的操作是創建一個正射投影矩陣,並且用這個矩陣乘以當前矩陣。其中近裁剪平面是一個矩形,矩形左下角點三維空間坐標是(left,bottom,-near),右上角點是(right,top,-near);遠裁剪平面也是一個矩形,左下角點空間坐標是(left,bottom,-far),右上角點是(right,top,-far)。所有的near和far值同時為正或同時為負。如果沒有其他變換,正射投影的方向平行於Z軸,且視點朝向Z負軸。這意味著物體在視點前面時far和near都為負值,物體在視點後面時far和near都為正值。
另一個函數是:
void gluOrtho2D(GLdouble left,GLdouble right,GLdouble bottom,GLdouble top)
它是一個特殊的正射投影函數,主要用於二維圖像到二維屏幕上的投影。它的near和far缺省值分別為-1.0和1.0,所有二維物體的Z坐標都為0.0。因此它的裁剪面是一個左下角點為(left,bottom)、右上角點為(right,top)的矩形。
(四)視口變換。
視口變換就是將視景體內投影的物體顯示在二維的視口平面上。運用相機模擬方式,我們很容易理解視口變換就是類似於照片的放大與縮小。在計算機圖形學中,它的定義是將經過幾何變換、投影變換和裁剪變換後的物體顯示於屏幕窗口內指定的區域內,這個區域通常為矩形,稱為視口。OpenGL中相關函數是:
glViewport(GLint x,GLint y,GLsizei width, GLsizei height);
這個函數定義一個視口。函數參數(x, y)是視口在屏幕窗口坐標系中的左下角點坐標,參數width和height分別是視口的寬度和高度。缺省時,參數值即(0, 0, winWidth, winHeight) 指的是屏幕窗口的實際尺寸大小。所有這些值都是以象素為單位,全為整型數。
(5)裁剪變換
在OpenGL中,除了視景體定義的六個裁剪平面(上、下、左、右、前、後)外,用戶還可自己再定義一個或多個附加裁剪平面,以去掉場景中無關的目標,如圖六所示。
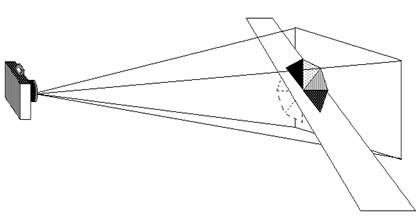
圖六、附加裁剪平面
附加平面裁剪函數為:
1、void glClipPlane(GLenum plane,Const GLdouble *equation);
函數參數equation指向一個擁有四個系數值的數組,這四個系數分別是裁剪平面Ax+By+Cz+D=0的A、B、C、D值。因此,由這四個系數就能確定一個裁剪平面。參數plane是GL_CLIP_PLANEi(i=0,1,...),指定裁剪面號。
在調用附加裁剪函數之前,必須先啟動glEnable(GL_CLIP_PLANEi),使得當前所定義的裁剪平面有效;當不再調用某個附加裁剪平面時,可用glDisable(GL_CLIP_PLANEi)關閉相應的附加裁剪功能。
下面這個例子不僅說明了附加裁剪函數的用法,而且調用了gluPerspective()透視投影函數,讀者可以細細體會其中的用法。例程如下:
#include "glos.h"
#include <GL/gl.h>
#include <GL/glu.h>
#include <GL/glaux.h>
void myinit(void);
void CALLBACK myReshape(GLsizei w, GLsizei h);
void CALLBACK display(void);
void CALLBACK display(void)
{
GLdouble eqn[4] = {1.0, 0.0, 0.0, 0.0};
glClear(GL_COLOR_BUFFER_BIT);
glColor3f (1.0, 0.0, 1.0);
glPushMatrix();
glTranslatef (0.0, 0.0, -5.0);
/* clip the left part of wire_sphere : x<0 */
glClipPlane (GL_CLIP_PLANE0, eqn);
glEnable (GL_CLIP_PLANE0);
glRotatef (-90.0, 1.0, 0.0, 0.0);
auxWireSphere(1.0);
glPopMatrix();
glFlush();
}
void myinit (void)
{
glShadeModel (GL_FLAT);
}
void CALLBACK myReshape(GLsizei w, GLsizei h)
{
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(60.0, (GLfloat) w/(GLfloat) h, 1.0, 20.0);
glMatrixMode(GL_MODELVIEW);
}
void main(void)
{
auxInitDisplayMode (AUX_SINGLE | AUX_RGB);
auxInitPosition (0, 0, 500, 500);
auxInitWindow ("Arbitrary Clipping Planes");
myinit ();
auxReshapeFunc (myReshape);
auxMainLoop(display);
}
(六)矩陣棧的操作
在講述矩陣棧之前,首先介紹兩個基本OpenGL矩陣操作函數:
1、void glLoadMatrix{fd}(const TYPE *m)
設置當前矩陣中的元素值。函數參數*m是一個指向16個元素(m0, m1, ..., m15)的指針,這16個元素就是當前矩陣M中的元素,其排列方式如下:
M = | m0 m4 m8 m12 |
| m1 m5 m9 m13 |
| m2 m6 m10 m14 |
| m3 m7 m11 M15 |
2、void glMultMatrix{fd}(const TYPE *m)
用當前矩陣去乘*m所指定的矩陣,並將結果存放於*m中。當前矩陣可以是用glLoadMatrix() 指定的矩陣,也可以是其它矩陣變換函數的綜合結果。
OpenGL的矩陣堆棧指的就是內存中專門用來存放矩陣數據的某塊特殊區域。一般說來,矩陣堆棧常用於構造具有繼承性的模型,即由一些簡單目標構成的復雜模型。矩陣堆棧對復雜模型運動過程中的多個變換操作之間的聯系與獨立十分有利。因為所有矩陣操作函數如glLoadMatrix()、glMultMatrix()、glLoadIdentity()等只處理當前矩陣或堆棧頂部矩陣,這樣堆棧中下面的其它矩陣就不受影響。堆棧操作函數有以下兩個:
·void glPushMatrix(void);
該函數表示將所有矩陣依次壓入堆棧中,頂部矩陣是第二個矩陣的備份;壓入的矩陣數不能太多,否則出錯。
·void glPopMatrix(void);
該函數表示彈出堆棧頂部的矩陣,令原第二個矩陣成為頂部矩陣,接受當前操作,故原頂部矩陣被破壞;當堆棧中僅存一個矩陣時,不能進行彈出操作,否則出錯。