問題描述
在給定大小的方格狀棋盤上, 將棋子”馬”放在指定的起始位置 , 棋子”馬” 的走子的規則為必須在棋盤上走”日”字; 從棋子”馬”的起始位置開始, 搜索出一條可行的路徑, 使得棋子”馬”能走遍棋盤上的所有落子點, 而且每個落子點只能走一次;
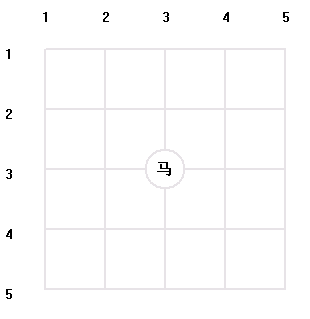
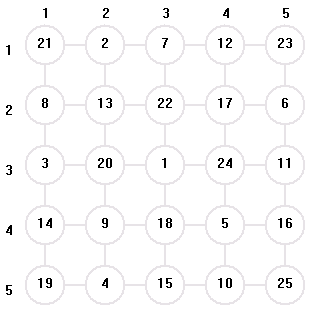
例如: 棋盤大小為5*5 , 棋子馬放的起始落子點為 ( 3 , 3 ) ; 算法需要搜索一條從位置( 3 , 3 ) 開始的一條包括從( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) … ( 5 , 1 ) , ( 5 , 2 ) , ( 5 , 3 ) , ( 5 , 4 ) , ( 5 , 5 ) 總共25個可以落子的全部位置;
問題分析
通過上面的問題描述,我們對問題的內容有了正確的理解,接下來我們開始對問題進行具體細致的分析,以求找到解決問題的正確的可行的合理的方法;
首先我們需要在程序中用合適的數據結構表示在問題中出現的棋盤 , 棋子 , 棋子的走子過程 ; 接下來我們需要對核心問題進行分析, 即如何搜索一條可行的路徑 , 搜索采取何種策略 , 搜索的過程如何表示 ;
對於一個大小為n*m大小的棋盤 , 棋子從當前位置( x , y ) 出發,可以到達的下一個位置( x’ , y’ ):
(1) ( x +1 , y +2 )
(2) ( x +1 , y –2 )
(3) ( x – 1, y +2 )
(4) ( x – 1, y – 2 )
(5) ( x +2, y +1)
(6) ( x +2, y – 1)
(7) ( x -2, y + 1)
(8) ( x -2, y – 1 )
限制條件:
1. 1 <= x’ <= n , 1 <= y’ <= m; ( n : 棋盤的高度 , m: 棋盤的寬度 );
2. ( x’ , y’ ) 必須是棋子記錄表中沒有包括的新位置;
3. 棋子走子過程記錄表中沒有包括棋盤上的所有可以落子的位置;
對這個過程不停迭代的過程也就是對解空間搜索的過程, 搜索直到棋子走子記錄表中包括棋盤上的所有可以落子的位置 , 就搜索到了一條可行的路徑,路徑包括棋盤上的所有落子點;或者搜索完整個解空間,仍然找不到一條可行的解,則搜索失敗;
下面我們舉例來說明搜索的過程;
棋盤大小 : 5 * 5
棋子起始位置 : ( 3 , 3 )
搜索過程 :
(1) 從當前位置( 3 , 3 )出發可以有8個新的位置選擇; 首先選擇新位置1 , 將新位置1
作為當前棋子位置 , 開始新的搜索;
如果搜索不成功, 則搜索回退, 選擇新位置2 ,以此類推,就可以搜索完整個解空間,只要從該問題有解 , 則可以保證一定可以搜索到;
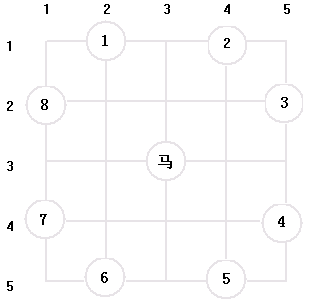
2) 從新位置1 開始新的搜索,可以選擇的新位置有兩個,先選擇位置1 , 從位置1開始新的搜索;
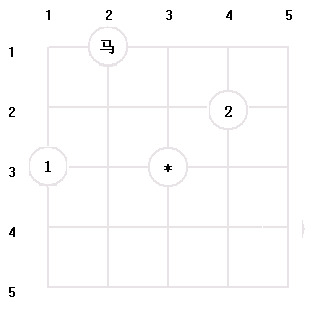
(3) 下圖是經過18步搜索之後的狀態, 從位置18出發, 已經沒有沒走過的新位置可以選擇, 則搜索失敗;
搜索回退到17步, 從位置17開始搜索除了18之外的新位置, 從圖上可以看出已經沒有新位置可以選擇,繼續回退到16步, 搜索除了17的新位置; 以此類推.知道搜索完整個解空間 , 或者搜索到一個可行解;
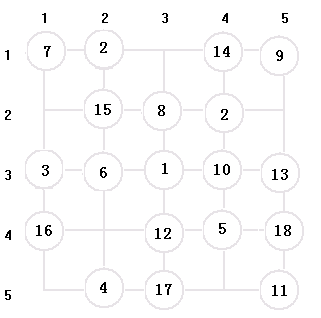
(4) 下圖展示了搜索成功的整個搜索過程;
系統設計
一. 用例圖
二. 類設計

三. 順序圖
四. 核心算法設計
通過上面的分析, 我們現在可以將算法的大概框架寫出來了 , 具體的代碼請參考本文章後面的源程序;
下面我們先列出了經典回溯算法的框架; 由於考慮到程序實現的方便性 , 所以本文中采用的回溯算法對經典算法進行了適當的修改;
經典算法:
void BackTrack( int t )本文采用的算法:
{
if ( t > n ) OutPut( x );
else
for( int I = f( n , k ) ; i <= g( n , k ) ; i ++ )
{
x[ t ] = h ( i );
if ( ConsTraint( t ) && Bound( k ) )
BackTrack( k + 1 );
}
}bool Search( Location curLoc )//開始計算;
{
m_complex++;
//修改棋盤標志;
m_chessTable[ curLoc.x-1 ][ curLoc.y-1 ] = 1;
//是否搜索成功結束標志;
if( isSuccess() )
return true;
//還有未走到的棋盤點,從當前位置開始搜索;
else
{
//遞歸搜索未走過的棋盤點;
for( int i = 0 ; i < 8 ; i++ )
{
Location newLocation = GetSubTreeNode( curLoc , i ) ;
if( isValide( newLocation ) &&
m_chessTable[newLocation.x-1][newLocation.y-1] == 0 )
{
if( Search( newLocation ) == true )
{
//填寫記錄表;
MarkInTable( newLocation, curLoc );
return true;
}
}
}
}
//搜索失敗,恢復棋盤標志;
m_chessTable[curLoc.x-1][curLoc.y-1] = 0;
return false;
}
測試數據和測試結果
(1). 測試數據1 :
棋盤大小 棋子起始位置 ( 1 , 1) ( 4 , 4 ) ( 2 , 3 ) 略… 搜索到的可行解 無 無 無 無 搜索解空間大小 2223 2223 501 略…
結論: 對於4 * 4 和小於 4*4的棋盤,此問題無可行解;
(2). 測試數據2:
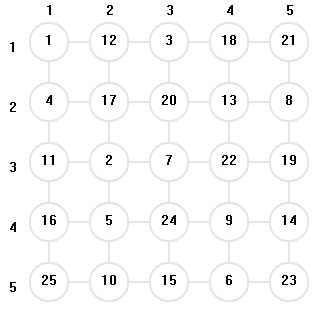
棋盤大小 : 5 * 5
棋子起始位置 : ( 1 , 1 )
搜索解空間大小 : 76497
搜索結果圖示 :

棋子起始位置 : ( 3 , 3 )
搜索解空間大小 : 11077
搜索結果圖示 :
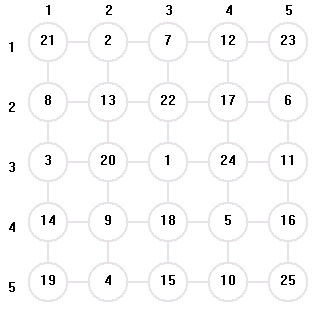
結論: 對於5*5 的棋盤 ,此問題有可行解,搜索解空間大小隨棋子的起始位置不同而不同,從某些位置起始搜索 , 此問題可能沒有可行解;
(3). 測試數據3 :
棋盤大小 : 6 * 6
棋子起始位置 : ( 4 , 2 )
搜索到的可行解 : 2029720
結果圖示 :
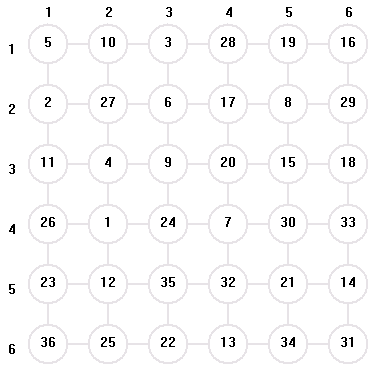
(4). 測試數據4:
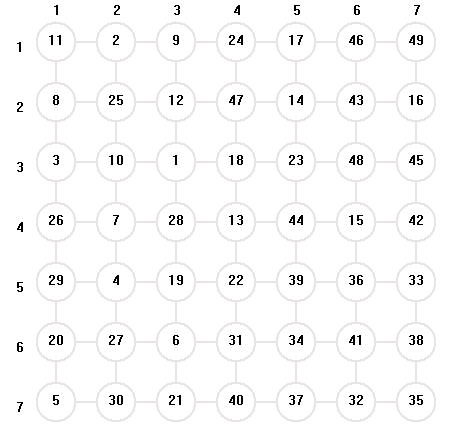
棋盤大小 : 7 * 7
棋子起始位置 : ( 3 , 3 )
搜索解空間大小 : 12799463
結果圖示 :
結論
通過多組數據的測試,我們發現當棋盤的高度 height <= 5 , 寬度 width <= 5 的時候, 該棋盤問題的解空間比較小,本文采用的算法可以在很短的時間內搜索完整個解空間 ;
當棋盤為5*5 大小 , 整個解空間大小為1829421 = 2 (21) ; 由於棋盤和棋子的一些特點 ( 如: 棋子從當前位置出發只能到達棋盤上的某些特殊點, 而且這些點必須不包含在走子記錄表中), 這就給分析棋盤算法的時間復雜度帶來了一些困難, 我們只能通過不同大小棋盤的特點來大概分析算法的時間復雜度, 通過實際的測試(在棋盤大小為5*5 ), 估算的時間復雜度與實際的復雜度基本在一個數量級;
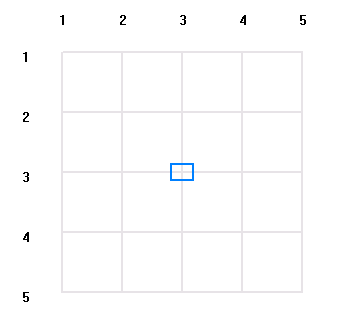
上圖是一個5*5大小的棋盤 , 方框所在的位置 ( 3 , 3 )出發可以到達的點有8個, 而下次從8個新的搜索點出發平均能到達的有2個點 , 還有25 – 1 – 8 = 16 個點 , 16個點中除去4個點就剩一般的點沒有走過, 從這4個點出發, 可以到達的新的搜索點平均有2個, 當棋盤上的一半以上的點全都走過,則從剩余的12個點出發可以到達的新的搜索點平均只有1;
通過上面的分析 , 我們可以得出 Space( 5*5 ) = 8 * pow( 2, 8 ) * pow( 2 , 4 ) * 12 = pow( 2 , 20 );
同理,我們可以對棋盤大小為8*8 的解空間大小進行估算; 當然估算當中的一些特殊點的選擇是需要一些技巧和實際經驗的, 雖然最終結果可能不准確 , 但是能夠保證基本在一個數量級上;
Space( 8 * 8 ) = pow( 4 , 8 ) * pow( 4 , 4 ) * pow( 2 , 20 ) * pow( 2 , 32 );
可以看出,解空間是相當大的, 我們假設計算機每分種搜索300萬步 , 對於棋子”馬”給定一個起始位置, 要想證明此問題無解 , 則需要搜索的時間為 ( 下面數字均為估計值 ) :
Time( 8 * 8 ) = Space ( 8 * 8 ) / 300萬 = pow( 2 , 76 ) / 300萬 = pow( 2 , 62 )分鐘 =
pow( 2 , 56 )天 = pow ( 2 , 47 )年 = 128億年
注: pow( x , y ) 代表x的y次方;
可見要搜索完一個大小為8*8 棋盤問題的全部解空間是根本不可能的;
算法的時間復雜度為pow( 2 , n ) , 是個NP難解問題;
具體算法實現請參考本文配套源代碼。
本文配套源碼