VC用遞歸的方法畫分形圖

分形幾何是數學領域裡新興的課題，如果將圖形的每個元素按某種規則進行變形，得到新的圖形，以此類推，進行若干次變形後得到的圖形就是分形圖形。Couch曲線是最典型的分形圖形：

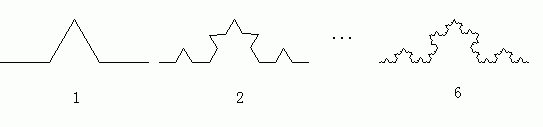
將一條線段按照圖1進行變換，得到圖1，再將圖1中的每條線段按圖1的折線變換得到圖2，以此類推，進行6次變換就得到圖6，如果進行無限次變換，就得到的是Couch曲線，Couch曲線的維數不是整數維，更多詳情請見分形方面的書籍。

用分形圖形能畫圖許多漂亮的圖案而被廣泛地應用，下面將幾個簡單的分形圖形的代碼與圖形大家分享。

//Couch曲線的畫法
void　Couch(CDC　*pDC,int　x1,int　y1,int　x2,int　y2,int　n)
{
//pDC是畫圖的設備上下文的指針
//x1,y1,x2,y2是起始的兩點
//其中參數n是遞歸的層數
int　x3,y3,x4,y4,x5,y5;
//以下是根據空間幾何計算出來的坐標
x3=x1+(x2-x1)/3;
y3=y1+(y2-y1)/3;
x4=x1+(x2-x1)*2/3;
y4=y1+(y2-y1)*2/3;
x5=x3+(x4-x3)/2+int(sqrt(3)*(y4-y3)/2);
y5=y3-int(sqrt(3)*(x4-x3)/2)+(y4-y3)/2;
//遞歸最後一層,遞歸的出口
if(n==1)
{
pDC->MoveTo(x1,y1);
pDC->LineTo(x3,y3);
pDC->LineTo(x5,y5);
pDC->LineTo(x4,y4);
pDC->LineTo(x2,y2);
}
else
{
//遞歸畫圖
Couch(pDC,x1,y1,x3,y3,n-1);
Couch(pDC,x3,y3,x5,y5,n-1);
Couch(pDC,x5,y5,x4,y4,n-1);
Couch(pDC,x4,y4,x2,y2,n-1);
}
}

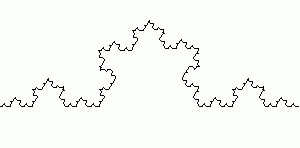
//斯賓斯基簍墊的畫法
void　Floor(CDC　*pDC,int　x1,　int　y1,int　x2,int　y2,int　x3,int　y3,int　n)
{
//pDC是畫圖的設備上下文的指針
//x1,y1,x2,y2,x3,y3是起始的三角形的三點坐標
//其中參數n是遞歸的層數
int　x11,x22,x33,y11,y22,y33;
//以下是根據空間幾何計算出來的坐標
x11=(x2+x3)/2;
y11=(y2+y3)/2;
x22=(x1+x3)/2;
y22=(y1+y3)/2;
x33=(x1+x2)/2;
y33=(y1+y2)/2;

pDC->MoveTo(x11,y11);
pDC->LineTo(x22,y22);
pDC->MoveTo(x11,y11);
pDC->LineTo(x33,y33);
pDC->MoveTo(x22,y22);
pDC->LineTo(x33,y33);
//遞歸最後一層,遞歸的出口
if(n==1)
{
pDC->MoveTo(x11,y11);
pDC->LineTo(x22,y22);
pDC->LineTo(x33,y33);
pDC->LineTo(x11,y11);
}
else
{
//遞歸畫圖
Floor(pDC,x1,y1,x33,y33,x22,y22,n-1);
Floor(pDC,x33,y33,x2,y2,x11,y11,n-1);
Floor(pDC,x22,y22,x11,y11,x3,y3,n-1);
}
}

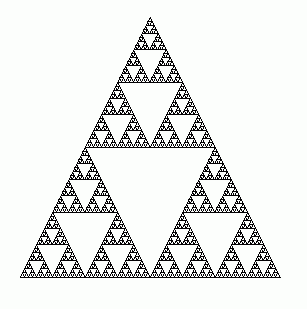
//分形矩形的畫法
void　Rect(CDC　*pDC,int　x1,int　y1,int　x2,int　y2,int　n)
{
//pDC是畫圖的設備上下文的指針
//x1,y1,x2,y2是起始矩形坐標
//其中參數n是遞歸的層數
int　x3,y3,x4,y4,x5,y5,x6,y6;
//以下是根據空間幾何計算出來的坐標
x3=x1+(x2-x1)/3;
y3=y1+(y2-y1)/3;
x4=x1+(x2-x1)*2/3;
y4=y1+(y2-y1)*2/3;
x5=x3+(y4-y3);
y5=y3-(x4-x3);
x6=x4-(y3-y4);
y6=y4+(x3-x4);

pDC->MoveTo(x1,y1);
pDC->LineTo(x3,y3);
pDC->MoveTo(x4,y4);
pDC->LineTo(x2,y2);
//遞歸最後一層,遞歸的出口
if(n==1)
{

pDC->MoveTo(x1,y1);
pDC->LineTo(x3,y3);
pDC->LineTo(x5,y5);
pDC->LineTo(x6,y6);
pDC->LineTo(x4,y4);
}
else
{
//遞歸畫圖
Rect(pDC,x3,y3,x5,y5,n-1);
Rect(pDC,x5,y5,x6,y6,n-1);
Rect(pDC,x6,y6,x4,y4,n-1);
}
}

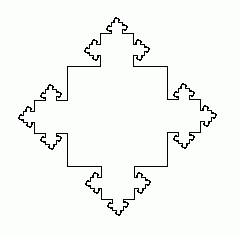
//分形樹的畫法，其中參數n是遞歸的層數
void　Tree(CDC　*pDC,int　x1,int　y1,int　x2,int　y2,int　n)
{
//pDC是畫圖的設備上下文的指針
//x1,y1,x2,y2是起始矩形坐標
//其中參數n是遞歸的層數
int　x3,y3,x4,y4,x5,y5;
//以下是根據空間幾何計算出來的坐標
x3=x1+(x2-x1)/3;
y3=y1+(y2-y1)/3;
x4=x3+int((x1-x3)*cos(5*pi/6))-int((y1-y3)*sin(5*pi/6));
y4=y3+int((x1-x3)*sin(5*pi/6))+int((y1-y3)*cos(5*pi/6));
x5=x3+int((x1-x3)*cos(5*pi/6))+int((y1-y3)*sin(5*pi/6));
y5=y3-int((x1-x3)*sin(5*pi/6))+int((y1-y3)*cos(5*pi/6));

pDC->MoveTo(x1,y1);
pDC->LineTo(x2,y2);
//遞歸最後一層,遞歸的出口
if(n==1)
{
pDC->MoveTo(x3,y3);
pDC->LineTo(x4,y4);
pDC->MoveTo(x3,y3);
pDC->LineTo(x5,y5);
}
else
{
//遞歸畫圖
Tree(pDC,x3,y3,x2,y2,n-1);
Tree(pDC,x3,y3,x4,y4,n-1);
Tree(pDC,x3,y3,x5,y5,n-1);
}
}

上述的代碼及圖形附有Visual C++源代碼，並在Windows XP和Visual C++6.0下調試成功。更多的分形圖形及圖形坐標空間幾何的計算方法請與作者聯系。