摘要
坐標變換是圖形學中很基本的操作。無論繪制二維還是三維圖形都會遇到。下面將會講到:
1、如何根據坐標架進行點的坐標變換
首先坐標架定義成:
struct PNT3D{
double x,y,z;
};
struct FRAME{
PNT3D O, OX, OY, OZ;
};
假設有一個點 p 定義在 frame 所在坐標系 WC(World Coordinate) 之中,也就是說 p 在 frame 之外。為了將 p 轉入 frame,我們首先需要作平移 p1 = p - frame.O; 這個時候 p1 相當於定義在一個將 WC 平移到 frame.O 的一個坐標架之中。這個坐標架和 frame.O 供用坐標原點,但是三個坐標軸並不一定相同。為了得到 frame 中的三個坐標分量我們只須將 p1 和三個基矢量作點積 :
WC->frame 變換公式:
p2.x = p1*frame.OX = (p-frame.O)*frame.OX;
p2.y = p1*frame.OY = (p-frame.O)*frame.OY;
p2.z = p1*frame.OZ = (p-frame.O)*frame.OZ;
其中 * 代表點積。這裡所得到的 p2 就是 WC 中的 p 在 frame 中對應的點。到此為止我們完成了電從坐標架之外變換到坐標架內。同樣的,我們也可以采用簡單的方法把點從坐標架內變換到坐標架之外。假設 p 是 frame 之內的點,首先
p1 = p.x*frame.OX + p.y*frame.OY + p.z*frame.OZ;
上面的公式將 p 的各個分量作為權值將三個坐標架的基矢量累加起來,得到的 p1 相當於平移 WC 和 frame 重合坐標原點的坐標架中的點。接下來,自然是處理平移
frame->WC 變換公式:
p2 = p1 + freame.O;
= p.x*frame.OX + p.y*frame.OY + p.z*frame.OZ + frame.O;
p2 就是轉換到 WC 的點。
2、如何根據坐標架生成變換矩陣
矩陣在圖形程序中應用十分廣泛。它可以表達更復雜的變換形式。這裡所指的矩陣是左乘矩陣,即矩陣位於點的左邊。
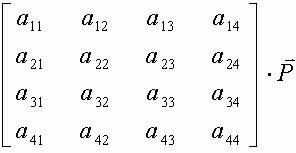
我們可以用一個矩陣來代表從坐標架外到坐標架中的變換,也可以用一個矩陣代表從坐標架之中到坐標架之外的變換。下面的 mat 是按照行優先規則存放的矩陣。從坐標架中變換到坐標架外 frame->WC 的矩陣如下 frame->WC 變換矩陣:
mat[0] = OX.x; mat[1] = OY.x; mat[2] = OZ.x; mat[3] = Oc.x;
mat[4] = OX.y; mat[5] = OY.y; mat[6] = OZ.y; mat[7] = Oc.y;
mat[8] = OX.z; mat[9] = OY.z; mat[10] = OZ.z; mat[11] = Oc.z;
mat[12] = 0; mat[13] = 0; mat[14] = 0; mat[15] = 1;
其中,OX, OY, OZ 是坐標架的三個基矢量,Oc 是坐標架的坐標原點。我們將這個矩陣乘以點 p(x,y,z,1)
p1 = mat*p;
我們可以得到 p1 就是 WC 坐標系下面的點。下面是這個矩陣的推導過程,如果覺得頭大,可以跳過去。
推導過程:
首先我們來看上面得到的根據一個坐標架,從坐標架內轉換到坐標架外的公式:
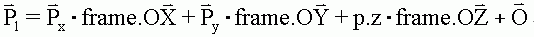
Px 是被轉換的點,P1 是轉換後的點。為了書寫方便,我們把 frame.OX 寫成 OX,其余類推。於是得到:
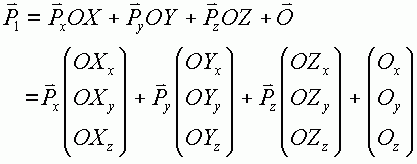
這個公式已經可以看到矩陣的影子了。為了進一步向 4*4 的矩陣靠近,我們采用齊次形式:
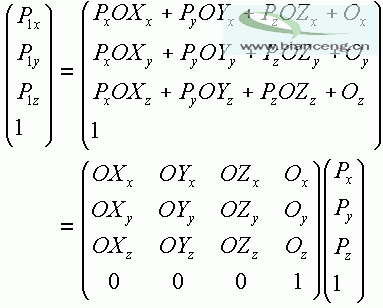
我們把它逐漸展開,我們就得到了這一大堆東西,這下子矩陣相乘的形式出來了。這裡的 4*4 的矩陣,就是上面的 mat 數組。
搞定了 frame->WC 的矩陣,我們現在來搞 WC->frame 的矩陣,
WC->frame 變換矩陣:
mat[0] = OX.x; mat[1] = OX.y; mat[2] = OX.z; mat[3] = -(Oc.x*OX.x + Oc.y*OX.y + Oc.z*OX.z);
mat[4] = OY.x; mat[5] = OY.y; mat[6] = OY.z; mat[7] = -(Oc.x*OY.x + Oc.y*OY.y + Oc.z*OY.z);
mat[8] = OZ.x; mat[9] = OZ.y; mat[10] = OZ.z; mat[11] = -(Oc.x*OZ.x + Oc.y*OZ.y + Oc.z*OZ.z);
mat[12] = 0; mat[13] = 0; mat[14] = 0; mat[15] = 1;
寫代碼的時候把這一堆抄過去就行了。如果不想看推導,就跳過下面的部分。
推導過程:
同樣的我們根據上面的式子出發進行推導:
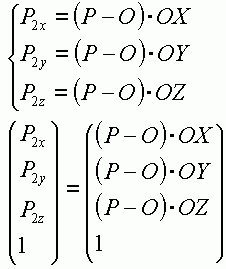
在這裡,我們把點也搞成了齊次形式,位的是更好的向 4*4 矩陣邁進。我們繼續拆解上面第二個式子的右面部分
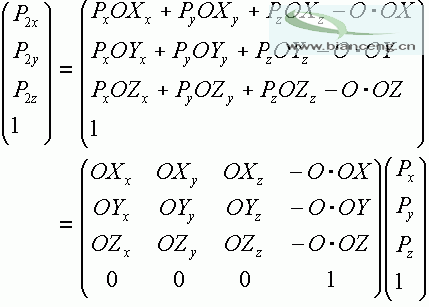
其實也很容易出來(不過炮炮是想了很長時間才想出來的:)。
3、如何通過矩陣作點的坐標變換
這個最好辦了。我們這裡討論的矩陣都是左乘矩陣,所以把矩陣乘以點就完成了變換。
x = M[0][0]*Px + M[0][1]*Py + M[0][2]*Pz + M[0][3];
y = M[1][0]*Px + M[1][1]*Py + M[1][2]*Pz + M[1][3];
z = M[2][0]*Px + M[2][1]*Py + M[2][2]*Pz + M[2][3];
這裡的 M 是一個 4*4 的二維數組,存放行優先的矩陣。
4、曲線、曲面方程如何作變換
曲線、曲面方程有參數方程、非參數方程等形式。當然曲線、曲面還可能由微分方程描述。這個時候微分方程如果沒有公式解,事情就很麻煩。計算機中一般比較容易處理參數方程。參數方程作變換形式上很簡單 。
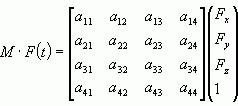
右邊的結果會得到一個矢量,最終可以得到 (F1x, F1y, F1z) 的形式,這是一個新的參數方程。如果曲線曲面由非參數方程描述 F(x,y,z)=0,比如
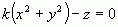
這個時候,你可以嘗試解出 x,y,z:
令 x = u,y = v,可以得到
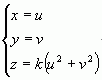
這下得到參數方程了,可以按照前面講的步驟作轉換。最後你會得到曲線、曲面變換後的參數方程。接下來你可以嘗試著消去這些中間參數 u,v。這個過程可能會比較艱難。
如果遇到隱式方程,無法解出,比如
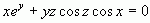
這是最倒霉的情況,求解是沒希望的。當然,如果你不要求精確的公式,你還是可以先令 x=u, y=v,代入之後,用泰勒展開求的 z 的級數,這也是一個方法哦:)