C#歸並排序的實現方法(遞歸,非遞歸,自然歸並)

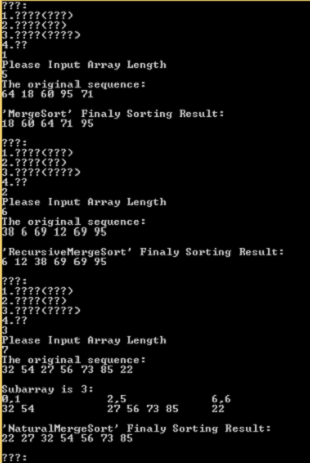
//Main:

代碼如下：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Merge
{
    class Program
    {
        static void Main(string[] args)
        {
            while (true)
            {
                Console.WriteLine("請選擇：");
                Console.WriteLine("1.歸並排序（非遞歸）");
                Console.WriteLine("2.歸並排序（遞歸）");
                Console.WriteLine("3.歸並排序（自然合並）");
                Console.WriteLine("4.退出");
                int Arraynum = Convert.ToInt32(Console.ReadLine());
                switch (Arraynum)
                {
                    case 4:
                        Environment.Exit(0);
                        break;
                    case 1:
                        Console.WriteLine("Please Input Array Length");
                        int Leng271 = Convert.ToInt32(Console.ReadLine());
                        Function obj1 = new Function(Leng271);

                        Console.WriteLine("The original sequence:");
                        Console.WriteLine(obj1);
                        Console.WriteLine("'MergeSort' Finaly Sorting Result:");
                        obj1.ToMergeSort();
                        Console.WriteLine(obj1);
                        break;
                    case 2:
                        Console.WriteLine("Please Input Array Length");
                        int Leng272 = Convert.ToInt32(Console.ReadLine());
                        Function obj2 = new Function(Leng272);

                        Console.WriteLine("The original sequence:");
                        Console.WriteLine(obj2);
                        Console.WriteLine("'RecursiveMergeSort' Finaly Sorting Result:");
                        obj2.ToRecursiveMergeSort();
                        Console.WriteLine(obj2);
                        break;
                    case 3:
                        Console.WriteLine("Please Input Array Length");
                        int Leng273 = Convert.ToInt32(Console.ReadLine());
                        Function obj3 = new Function(Leng273);

                        Console.WriteLine("The original sequence:");
                        Console.WriteLine(obj3);
                        obj3.ToNaturalMergeSort();
                        Console.WriteLine();Console.WriteLine();
                        Console.WriteLine("'NaturalMergeSort' Finaly Sorting Result:");
                        Console.WriteLine(obj3);
                        break;
                }
            }
        }
    }
}

//Class:

代碼如下：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Merge
{
    // 【example 2.7】//抱歉，實在不知怎麼學習英語，語法什麼錯誤之處還請見諒。
    class Function
    {
        private int Groups;
        private int CopyGroups;
        private int mergerows;
        private int[] Array27;
        private static Random ran = new Random();
        public Function(int length)
        {
            Array27 = new int[length];
            for (int i = 0; i < length; i++)
                Array27[i] = /*Convert.ToInt32(Console.ReadLine()); //*/ran.Next(1, 100);
        }
        //選擇
        public void ToMergeSort()
        {
            MergeSort(Array27);
        }
        public void ToRecursiveMergeSort()
        {
            RecursiveMergeSort(Array27, 0, Array27.Length - 1);
        }
        public void ToNaturalMergeSort()
        {
            NaturalMergeSort(Array27);
        }

        /// <summary>
        /// 歸並排序(遞歸）
        ///    核心思想：（分治）
        ///           將待排序元素（遞歸直至元素個數為１）分成左右兩個大小大致相同的2個子集合，然後，
        ///           分別對2個子集合進行排序，最終將排好序的子集合合並成為所要求的排好序的集合． 
        /// 核心算法時間復雜度：  
        ///           T(n)=O(nlogn)
        /// 參考 優秀代碼: http://zh.wikipedia.org/wiki/%E5%90%88%E4%BD%B5%E6%8E%92%E5%BA%8F
        ///               http://www.cnblogs.com/mingmingruyuedlut/archive/2011/08/18/2144984.html
        /// </summary>
        /// <param name="Array"></param>
        /// <param name="left"></param>
        /// <param name="right"></param>
        public void RecursiveMergeSort(int[] Array, int left, int right)
        {
            int middle = (left + right) / 2;

            if (left < right)
            {
                //對前半部分遞歸拆分
                RecursiveMergeSort(Array, left, middle);
                //對後半部分遞歸拆分
                RecursiveMergeSort(Array, middle + 1, right);
                MergeOne(Array, left, middle, right);
            }
        }
        public void MergeOne(int[] Array, int left, int middle, int right)
        {
            int leftindex = left;
            int rightindex = middle + 1;
            //動態臨時二維數組存放分割為兩個小Array的數組排列順序後的數據
            int[] merge = new int[right + 1];
            int index = 0;
            //對兩個小數組合並排序
            while (leftindex <= middle && rightindex <= right)
                merge[index++] = (Array[leftindex] - Array[rightindex]) >= 0 ? Array[rightindex++] : Array[leftindex++];
            //有一側子數列遍歷完後，將另外一側子數列剩下的數依次放入暫存數組中（有序）
            if (leftindex <= middle)
            {
                for (int i = leftindex; i <= middle; i++)
                    merge[index++] = Array[i];
            }
            if (rightindex <= right)
            {
                for (int i = rightindex; i <= right; i++)
                    merge[index++] = Array[i];
            }
            //將有序的數列 寫入目標數組 ，即原來把Array數組分為兩個小Array數組後重新有序組合起來(覆蓋原數組）
            index = 0;
            for (int i = left; i <= right; i++)
                Array[i] = merge[index++];
        }

        /// <summary>
        /// 歸並排序(非遞歸）
        ///     核心思想：（分治）
        ///           對n個數的數列每相鄰兩個元素排序，組成n/2個或（n+1)/2個子數組，單個的不比了直接進入下一輪。
        ///     然後對每個相鄰的子數組再排序，以此類推最後得到排好序的數列
        ///  forexample：  59 35 54 28 52
        ///   排序And分：  35 59. 28 54. 52
        ///   排序And分：  28 35 54 59. 52
        ///        結果：  28 35 52 54 59
        /// 核心算法時間復雜度：  
        ///           T(n)=O(nlogn)
        /// </summary>
        /// <param name="Array"></param>
        public void MergeSort(int[] Array)
        {
            //index固定的數組
            int[] merge = new int[Array.Length];
            int P = 0;
            while (true)
            {
                int index = 0;
                //子數組元素的個數
                int ENumb = (int)Math.Pow(2, P);
                //一個子數組中的元素個數與數組的一半元素個數比較大小
                //最糟糕的情況最右邊的數組只有一個元素
                if (ENumb < Array.Length)
                {
                    while (true)
                    {
                        int TorFAndrightindex = index;
                        //最後一個子數組的第一個元素的index與數組index相比較
                        if (TorFAndrightindex <= Array.Length - 1)
                            MergeTwo(Array, merge, index, ENumb);
                        else
                            break;
                        index += 2 * ENumb;
                    }
                }
                else
                    break;
                P++;
            }
        }
        public void MergeTwo(int[] Array, int[] merge, int index, int ENumb)
        {
            //換分兩個子數組的index(千萬不能用middle = (right + left) / 2劃分）
            // 1
            int left = index;
            int middle = left + ENumb - 1;
            //（奇數時）
            //排除middleindex越界
            if (middle >= Array.Length)
            {
                middle = index;
            }
            //同步化merge數組的index
            int mergeindex = index;
            // 2
            int right;
            int middleTwo = (index + ENumb - 1) + 1;
            right = index + ENumb + ENumb - 1;
            //排除最後一個子數組的index越界.
            if (right >= Array.Length - 1)
            {
                right = Array.Length - 1;
            }
            //排序兩個子數組並復制到merge數組
            while (left <= middle && middleTwo <= right)
            {
                merge[mergeindex++] = Array[left] >= Array[middleTwo] ? Array[middleTwo++] : Array[left++];
            }
            //兩個子數組中其中一個比較完了（Array[middleTwo++] 或Array[left++]），
            //把其中一個數組中剩下的元素復制進merge數組。
            if (left <= middle)
            {
                //排除空元素.
                while (left <= middle && mergeindex < merge.Length)
                    merge[mergeindex++] = Array[left++];
            }
            if (middleTwo <= right)
            {
                while (middleTwo <= right)
                    merge[mergeindex++] = Array[middleTwo++];
            }
            //判斷是否合並至最後一個子數組了
            if (right + 1 >= Array.Length)
                Copy(Array, merge);
        }

        /// <summary>
        /// 自然歸並排序:
        ///      對於初始給定的數組,通常存在多個長度大於1的已自然排好序的子數組段.
        /// 例如,若數組a中元素為{4,8,3,7,1,5,6,2},則自然排好序的子數組段
        /// 有{4,8},{3,7},{1,5,6},{2}.
        /// 用一次對數組a的線性掃描就足以找出所有這些排好序的子數組段.
        /// 然後將相鄰的排好序的子數組段兩兩合並,
        /// 構成更大的排好序的子數組段({3,4,7,8},{1,2,5,6}).
        /// 繼續合並相鄰排好序的子數組段,直至整個數組已排好序.
        /// 核心算法時間復雜度：
        ///        T(n)=○(n);
        /// </summary>
        public void NaturalMergeSort(int[] Array)
        {
            //得到自然劃分後的數組的index組（每行為一個自然子數組）
            int[,] PointsSymbol = LinearPoints(Array);
            //子數組只有一個。
            if (PointsSymbol[0, 1] == Array.Length - 1)
                return;
            //多個(至少兩個子數組）...
            else
                //可以堆棧調用嗎？
                NaturalMerge(Array, PointsSymbol);

        }
        public void NaturalMerge(int[] Array, int[,] PointsSymbol)
        {
            int left;
            int right;
            int leftend;
            int rightend;

            mergerows = GNumberTwo(Groups);
            CopyGroups = Groups;
            //固定狀態
            int[] TempArray = new int[Array.Length];
            //循環取每個自然子數組的index
            while (true)
            {
                // int Temprow = 1;
                //只記錄合並後的子數組(”《應該為》“動態的） 
                int[,] TempPointsSymbol = new int[mergerows, 2];

                int row = 0;
                do
                {
                    //最重要的判斷：最後(一組子數組)是否可配對
                    if (row != CopyGroups - 1)
                    { //以上條件也可以含有(& 和&&的區別)短路運算
                        //參考:http://msdn.microsoft.com/zh-cn/library/2a723cdk(VS.80).aspx
                        left = PointsSymbol[row, 0];
                        leftend = PointsSymbol[row, 1];
                        right = PointsSymbol[row + 1, 0];
                        rightend = PointsSymbol[row + 1, 1];
                        MergeThree(Array, TempArray, left, leftend, right, rightend);
                        MergePointSymbol(PointsSymbol, TempPointsSymbol, row);
                    }
                    else
                    {
                        ////默認剩下的單獨一個子數組已經虛擬合並。然後Copy進TempArray。
                        int TempRow = PointsSymbol[row, 0];
                        int TempCol = PointsSymbol[row, 1];
                        while (TempRow <= TempCol)
                            TempArray[TempRow] = Array[TempRow++];
                        //TempPointSymbol完整同步
                        TempPointsSymbol[row / 2, 0] = PointsSymbol[row, 0];
                        TempPointsSymbol[row / 2, 1] = PointsSymbol[row, 1];
                        break;//重新開始新一輪循環。
                    }
                    row += 2;
                    // Temprow++;
                    //合並到只有一個子數組時結束循環
                    if (TempPointsSymbol[0, 1] == Array.Length - 1)
                        break;
                }//判斷別進入越界循環(可以進孤單循環）這裡指的是PointsSymbol的子數組個數
                while (row <= CopyGroups - 1);
                //
                Copy(Array, TempArray);
                //更新子數組index，row為跳出循環的條件（最後單個子數組或下一個越界的第一個）
                UpdatePointSymbol(PointsSymbol, TempPointsSymbol, row);
                //改變TempPointsSymbol的行數（合並後子數組數）
                mergerows = GNumber(mergerows);
                CopyGroups = GNumberTwo(CopyGroups);
                //合並到只有一個子數組時結束循環
                if (PointsSymbol[0, 1] == Array.Length - 1)
                    break;
            }
            //輸出
        }
        public int GNumber(int Value)
        {
            if (Value % 2 == 0)
                Value /= 2;
            else
                Value -= 1;

            return Value;
        }
        public int GNumberTwo(int Value)
        {
            if (Value % 2 == 0)
                mergerows = Value / 2;
            else
                mergerows = Value / 2 + 1;
            return mergerows;
        }
        public void MergeThree(int[] Array, int[] Temp, int left, int leftend, int right, int rightend)
        {
            //合並語句
            int index = left;
            while (left <= leftend && right <= rightend)
                Temp[index++] = Array[left] >= Array[right] ? Array[right++] : Array[left++];
            while (left <= leftend)
                Temp[index++] = Array[left++];
            while (right <= rightend)
                Temp[index++] = Array[right++];
        }
        public void MergePointSymbol(int[,] PointsSymbol, int[,] TempPointsSymbol, int row)
        {
            int rowindex = row / 2;
            TempPointsSymbol[rowindex, 0] = PointsSymbol[row, 0];
            TempPointsSymbol[rowindex, 1] = PointsSymbol[row + 1, 1];
        }
        public void UpdatePointSymbol(int[,] PointsSymbol, int[,] TempPointsSymbol, int rows)
        {
            int row = 0;
            //if (mergerows % 2 == 0)
            //{
            for (; row < TempPointsSymbol.GetLength(0); row++)
            {
                for (int col = 0; col < 2; col++)
                    PointsSymbol[row, col] = TempPointsSymbol[row, col];
            }
            //後面的清零
            for (; row < PointsSymbol.GetLength(0); row++)
            {
                for (int col2 = 0; col2 < 2; col2++)
                    PointsSymbol[row, col2] = 0;
            }
            //}
            ////補剩下的index組，
            //else
            //{
            //    for (int row2 = 0; row2 < TempPointsSymbol.GetLength(0); row2++)
            //    {
            //        for (int col3 = 0; col3 < 2; col3++)
            //            PointsSymbol[row2, col3] = TempPointsSymbol[row2, col3];
            //    }
            //    //最後一個子數組的index只有一個。
            //    int row3 = TempPointsSymbol.GetLength(0);
            //    PointsSymbol[row3, 0] = PointsSymbol[rows, 0];
            //    PointsSymbol[row3, 1] = PointsSymbol[rows, 1];
            //    //後面的清零
            //    for (int row4 = row3 + 1; row4 < PointsSymbol.GetLength(0); row4++)
            //    {
            //        for (int col4 = 0; col4 < 2; col4++)
            //            PointsSymbol[row4, col4] = 0;
            //    }
            //}

        }
        public int[,] LinearPoints(int[] Array)
        {
            Groups = 1;
            int StartPoint = 0;
            int row = 0;
            int col = 0;
            //最糟糕的情況就是有Array.Length行。
            int[,] PointsSet = new int[Array.Length, 2];
            //線性掃描Array，劃分數組
            //初始前index=0
            PointsSet[row, col] = 0;
            do
            {
                //判斷升序子數組最終的index開關
                bool Judge = false;
                //從Array第二個數判斷是否要結束或者是否是升序子數組.
                while (++StartPoint < Array.Length && Array[StartPoint] < Array[StartPoint - 1])
                {
                    //打開第一個升序子數組結束的index開關
                    Judge = true;
                    //重新開始第二個升序子數組的前index
                    PointsSet[row, col + 1] = StartPoint - 1;
                    //計算子數組個數
                    Groups++;
                    //換行記錄自然子數組的index
                    row++;
                    break;
                    //--StartPoint;
                }
                //升序子數組結束index
                if (Judge)
                    PointsSet[row, col] = StartPoint;
                //else
                //    --StartPoint;
            } while (StartPoint < Array.Length);
            //最終index=StartPoint - 1，但是糟糕情況下還有剩余若干行為： 0,0 ...
            PointsSet[row, col + 1] = StartPoint - 1;
            //調用展示方法          
            DisplaySubarray(Array, PointsSet, Groups);
            return PointsSet;
        }
        public void DisplaySubarray(int[] Array, int[,] PointsSet, int Groups)
        {
            Console.WriteLine("Subarray is {0}:", Groups);
            //展示子數組的前後index
            for (int r = 0; r < Groups; r++)
            {
                for (int c = 0; c < PointsSet.GetLength(1); c++)
                {
                    Console.Write(PointsSet[r, c]);
                    if (c < PointsSet.GetLength(1) - 1)
                        Console.Write(",");
                }
                Console.Write("\t\t");
            }
            Console.WriteLine();
            //展示分出的子數組
            for (int v = 0; v < Groups; v++)
            {
                int i = 1;
                for (int r = PointsSet[v, 0]; r <= PointsSet[v, 1]; r++)
                {
                    Console.Write(Array[r] + " ");
                    i++;
                }
                if (i <= 3)
                    Console.Write("\t\t");
                else
                    Console.Write("\t");
                if (PointsSet[v, 1] == Array.Length)
                    break;
            }
        }

        public void Copy(int[] Array, int[] merge)
        {
            //一部分排好序的元素替換掉原來Array中的元素
            for (int i = 0; i < Array.Length; i++)
            {
                Array[i] = merge[i];
            }
        }
        //輸出
        public override string ToString()
        {
            string temporary = string.Empty;

            foreach (var element in Array27)
                temporary += element + " ";

            temporary += "\n";
            return temporary;
        }
    }
}