C# 排序算法之堆排序

一、基本概念

堆：這裡是指一種數據結構，而不是我們在C#中提到的用於存儲引用類型對象的地方。它可以被當成一棵完全二叉樹。
 
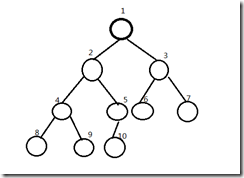
為了將堆用數組來存放，這裡對每個節點標上順序。事實上，我們可以用簡單的計算公式得出父節點，左孩子，右孩子的索引：

    parent(i) =

    left(i) = 2i

    right(i)=2i + 1

最大堆和最小堆: 最大堆是指所有父節點的值都大於其孩子節點的堆，即滿足以下公式：

                      A[parent[i]]A[i](A是指存放該堆的數組)

    最小堆相反。

    最大堆和最小堆是堆排序的關鍵，可知最大堆的根節點是堆中最大的節點。因此只要我們構造出最大(小)堆，最大(小)的元素也就得到了，然後再對剩下的元素繼續構造最大(小)堆，就可以取出第二大(小)的元素，依此類推，直到排序完成。

二、構造最大(小)堆
我們已經得知構造最大(小)堆是堆排序的關鍵，下面就來看看如何構造最大堆。
萬事開頭難，首先來看一種特殊的情形吧：堆的根節點的左子樹和右子樹都已經是最大堆了，然而根節點卻比孩子節點小，當然，這個堆不滿足最大堆的定義。為了⑩這個堆成為最大堆，我們可以按如下步驟操作：
（1）將根節點與左右孩子中最大的交換
（2）交換之後可能會面臨左或右子樹不是最大堆的問題，但由於整個左(右)子樹一開始就是最大堆，問題又回到了最開始的狀態，因此只要如此反復即可得到最大堆。
對於上面的特殊堆已經找到了解決辦法，但對於一般意義上的堆呢？
我們可以選擇自底向上來構造：葉子節點是特殊的最大堆，舉個例子有葉子節點a,b,它們的父節點是p;a,b肯定已經是最大堆了，這是要保證a,b,p組成的子樹是最大堆。這個堆很眼熟是不是？沒錯，它就是前面提到的特殊的堆。在a,b,p組成的子樹變成最大堆後，我們又可以類似的使該子樹，該子樹的父節點，以及同胞子樹（或節點）組成的新子樹成為最大堆，如此類推，最終使堆變為最大堆。

對於求解最小堆與此類似。
三、實現
完整代碼:
代碼如下：

namespace HeapSort
{
using System;
class Program
{
static int heapSize =0;
static void Main(string[] args)
{
var heap = new[] { -1, 10, 5, 12, 77, 54, 7, 34, 23, 11 };//為了方便，索引0處不存放元素（或存放無用元素）
heapSize = heap.Length - 1;
BuildMaxHeap(heap);
for (var i = heap.Length - 1; i >= 2; i--)
{
//1.每次在構建好最大堆後，將第一個元素和最後一個元素交換；
//2.第一次以索引1到length-1出的元素組成新的堆，第二次1到length-2，直到剩下最後兩個元素組成堆
//3.每次新組成的堆除了根節點其他節點都能保持最大堆的特性，因此只要DoBuildMaxHeap(heap, 1)就可以得到新的最大堆
Swap(heap, 1, i);
heapSize--;
MaxHeapfy(heap, 1);
}
foreach (var i in heap)
Console.Write(i + " ");
}
static void BuildMaxHeap(int[] heap)
{
for (var i = (heap.Length - 1) / 2; i >= 1; i--)
{
MaxHeapfy(heap, i);
}
}
static void MaxHeapfy(int[] heap, int index)
{
var largerItemIndex = index;
var leftChildIndex = index << 1;
var rightChildIndex = (index<<1) + 1;
if (leftChildIndex <= heapSize && heap[leftChildIndex] > heap[index])
{
largerItemIndex = leftChildIndex;
}
if (rightChildIndex <= heapSize && heap[rightChildIndex] > heap[largerItemIndex])
{
largerItemIndex = rightChildIndex;
}
if( index != largerItemIndex)
{
Swap(heap, index, largerItemIndex);
MaxHeapfy(heap, largerItemIndex);
}
}
static void Swap(int[] heap, int index1, int index2)
{
var temp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = temp;
}
}
}

1.MaxHeapfy:該方法的前提是index處節點的左右子樹已經是最大堆，最終的目的是使以index處節點為根的堆成為最大堆

2.BuildMaxHeap：該方法涉及一個事實：如果一個對含n個元素，那麼從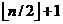開始的元素（假設節點下表從1開始）就一定是葉子節點（這一點可以用反證法證明，假設處節點不是葉子節點，那麼該節點必包含子節點，從而可以得出其左孩子的索引2 *() > n的結論，顯然這是錯誤的）。在這個前提下，該方法至底向上通過MaxHeapfy將堆構建成最大堆。