前幾天在博客園看到有人面試時,遇到遞歸算法題,一時手癢就解了一個。順便網上又找來幾個,也實現了。給大家分享一下,開闊一下思路,沒准你明天面試就能用上。
1、編寫一個方法用於驗證指定的字符串是否為反轉字符,返回true和false。請用遞歸算法實現。(反轉字符串樣式為"abcdedcba")
2、一列數的規則如下: 1、1、2、3、5、8、13、21、34...... 求第30個是多少
3、一列數的規則如下: 1、12、123、1234、12345、123456......,求第n個數的遞歸算法(n<=9)。
4、將一整數逆序,如987654321變為123456789。
5、一個射擊運動員打靶,靶一共有10環,連開10槍打中90環的可能行有多少種?
以上的前提:不能用數組 或轉成字符串處理,也不能用內置函數,如C#的冪函數(Math.Pow)
using System;
namespace RecursionAlgorithms
{
class Program
{
private static bool fn1(ref string str, ref int from, ref int to)
{
if (from >= to) return true;
if (str[from++] != str[to--]) return false;
return fn1(ref str, ref from, ref to);
}
private static int fn2(int i)
{
return i <= 2 ? 1 : fn2(i - 2) + fn2(i - 1);
}
private static long fn3(long x, ref long n)
{
return (x <= 1) ? x : fn3(x - 1, ref n) + x * (n *= 10);
}
private static long fn4(long x, ref long n)
{
return (x < 10) ? x : fn4(x / 10, ref n) + (x % 10) * (n *= 10);
}
private static long fn5(int n, int sum)
{
if ((n == 1 && sum <= 10) || (sum == n * 10)) return 1;
if (sum > n * 10 || sum < 0) return 0;
long ok = 0;
for (int i = 0; i <= 10; i++)
{
ok += fn5(n - 1, sum - i);
}
return ok;
}
static void Main(string[] args)
{
string[] strs = { "", "a", "aa", "aba", "abba", "abcba", "ab", "abc", "abca" };
for (int i = 0; i < strs.Length; i++)
{
string str = strs[i];
int from = 0, to = str.Length - 1;
Console.WriteLine("{0} is {1}", str, fn1(ref str, ref from, ref to));
}
for (int i = 1; i <= 30; i++) Console.Write("{0}:{1} \t", i, fn2(i));
long n = 1, m = 1, t = 0;
for (int i = 0; i <= 9; i++, n = m = 1)
{
Console.Write("\n {0} ==> {1}", t = fn3(i, ref n), fn4(t, ref m));
}
Console.WriteLine("\n{0}種可能性", fn5(10, 90));
}
}
}
測試一下:
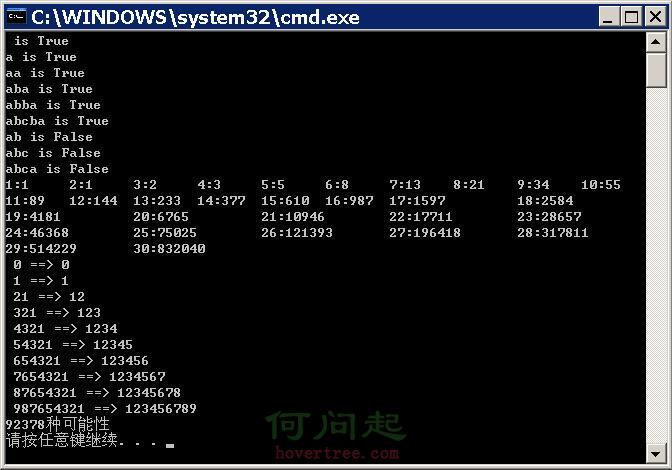
遞歸算法很有意思的,並不是說函數調用自身就一定是遞歸算法。有一次我做面試官,有一童鞋在一道簡單的遞歸函數中,還用到了for循環,當場被我Pass(當然還有其他因素)
總結一下遞歸算法的解題思路:
首先步驟分解,寫出最後一次遞歸(n=1)的計算公式,然後是倒數第二次(n=2),n=3....,最後歸納出遞歸算法
如第二題:fn(1)=1;f(2)=1;f(3)=f(1)+f(2);----> f(n)=f(n-2)+f(1),那麼很容易就寫出這個遞歸函數
f(n)={n<=2?1:fn(n-2)+f(n-1)}
再如第五題: 遞歸函數定義:f(n,sum),n:輪次,sum:本輪及本輪之後應打中的總環數,返回值0代表一次失敗的組合,返回值大於0則代表滿足題設情況的組合數量。 f(1,sum),sum<0||sum>10,則返回0; sum<=10,這說明最後一槍只要打中sum環,就能滿足題設,返回1,即一次組合情況 f(2,sum),sum<0||sum>20,則返回0; sum==20,這說明最後兩槍只要打都中10環,就能滿足題設,返回1 sum<20,如果倒數第二槍打中x環[0,10],最後一槍打中sum-x環,也就能滿足題設,成功情況累加 注意這裡,上一句就可以描述為:當本輪打中x環的情況下,後幾輪能打中sum-x環的情況能有幾種,也即f(n-1,sum-x)種情況 我這個遞歸算法中,還可以加上一個數組參數用來記錄前幾輪的中靶情況,這樣就能打印出每種組合 在遞歸算法中,當遞歸層次很深時,要考慮空間復雜度,盡量減少新變量,所以我的算法中,多用了ref方式。在面試可以忽略這種情況,加快解題速度。 另外,多數遞歸算法都可以拆解成非遞歸的循環算法,因為這樣會減少遞歸函數的入棧出棧。在實際運用中,要綜合考慮運行工況(CPU、內存、算法被調用的頻度,遞歸層數等),也就是空間與時間的取捨。