首先結果是:
public bool IsPowerOfTwo(int n) {
if(n<1) return false;//2的次冪一定大於0
return ((n & (n -1)) == 0);
}
分析:2的次冪在計算機中可以用左移(<<)來運算,了解n&(n-1)的作用如下:
n&(n-1)作用:將n的二進制表示中的最低位為1的改為0,先看一個簡單的例子:
n = 10100(二進制),則(n-1) = 10011 ==》n&(n-1) = 10000
可以看到原本最低位為1的那位變為0。
弄明白了n&(n-1)的作用,那它有哪些應用?
1. 求某一個數的二進制表示中1的個數
while (n >0 ) {
count ++;
n &= (n-1);
}
2. 判斷一個數是否是2的方冪
n > 0 && ((n & (n - 1)) == 0 )
3. 計算N!的質因數2的個數。
容易得出N!質因數2的個數 = [N / 2] + [N / 4] + [N / 8] + ....
下面通過一個簡單的例子來推導一下過程:N = 10101(二進制表示)
現在我們跟蹤最高位的1,不考慮其他位假定為0,
則在
[N / 2] 01000
[N / 4] 00100
[N / 8] 00010
[N / 8] 00001
則所有相加等於01111 = 10000 - 1
由此推及其他位可得:(10101)!的質因數2的個數為10000 - 1 + 00100 - 1 + 00001 - 1 = 10101 - 3(二進制表示中1的個數)
推及一般N!的質因數2的個數為N - (N二進制表示中1的個數)
目前看到只有這些應用,但只要理解了n&(n-1)的原理及作用,在碰到相關問題時也會比較容易解決。
原文:http://6460646.blog.163.com/blog/static/27779875201132893614412/
int n = 16;//一定是大於0的
以下是在C#中 整數的各進制的轉化
var x = 2;
Console.WriteLine("n的"+x+"進制為:"+Convert.ToString(n,x)+";n-1的2進制:"+Convert.ToString(n-1,x));
x = 8;
Console.WriteLine("n的" + x + "進制為:" + Convert.ToString(n, x) + ";n-1的2進制:" + Convert.ToString(n - 1, x));
x = 10;
Console.WriteLine("n的" + x + "進制為:" + Convert.ToString(n, x) + ";n-1的2進制:" + Convert.ToString(n - 1, x));
x = 16;
Console.WriteLine("n的" + x + "進制為:" + Convert.ToString(n, x) + ";n-1的2進制:" + Convert.ToString(n - 1, x));
var b = n&(n-1);
Console.WriteLine(b);
ps:& 運算符如果不清楚可以和我私聊或者留言
二進制與十進制的相互轉換的手動演算如下:
轉成二進制主要有以下幾種:正整數轉二進制,負整數轉二進制,小數轉二進制;
1、 正整數轉成二進制。要點一定一定要記住哈:除二取余,然後倒序排列,高位補零。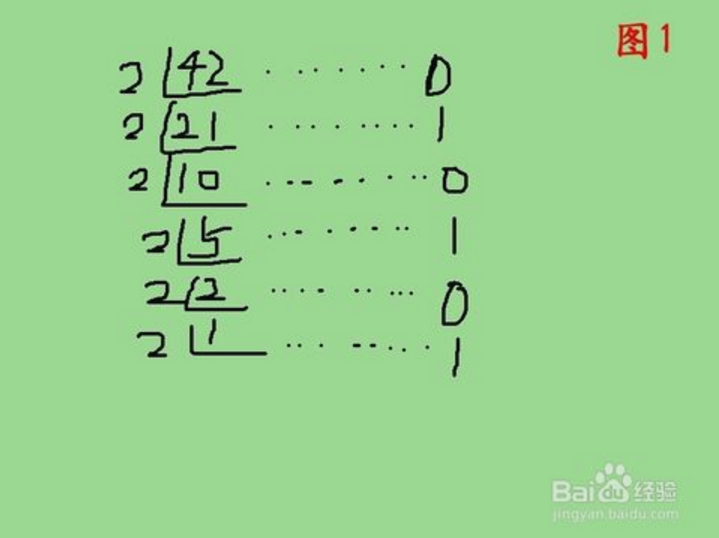
2.42除以2得到的余數分別為010101,然後咱們倒著排一下,42所對應二進制就是101010.如圖2所示更直觀的表達。
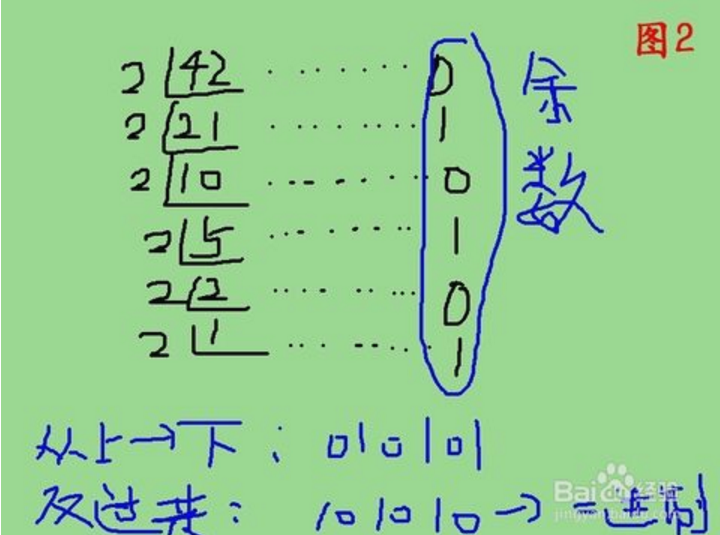
3.計算機內部表示數的字節單位是定長的,如8位,16位,或32位。所以,位數不夠時,高位補零,所說,如圖3所示,42轉換成二進制以後就是。00101010,也即規范的寫法為(42)10=(00101010)2.趕緊記住吧。
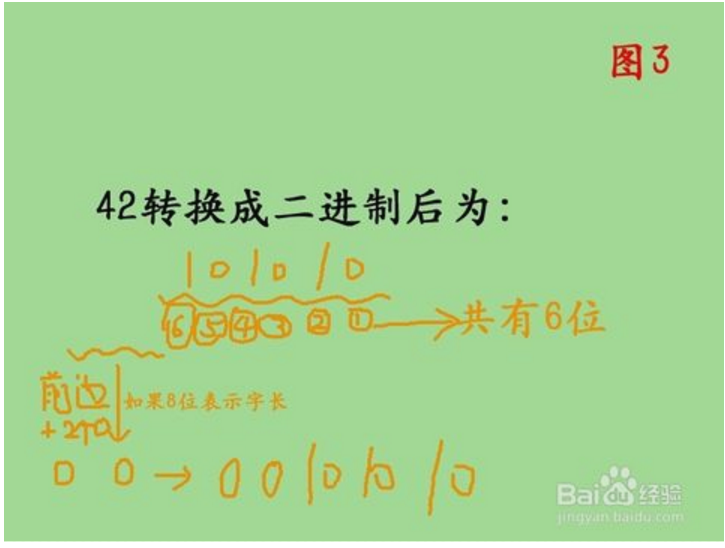
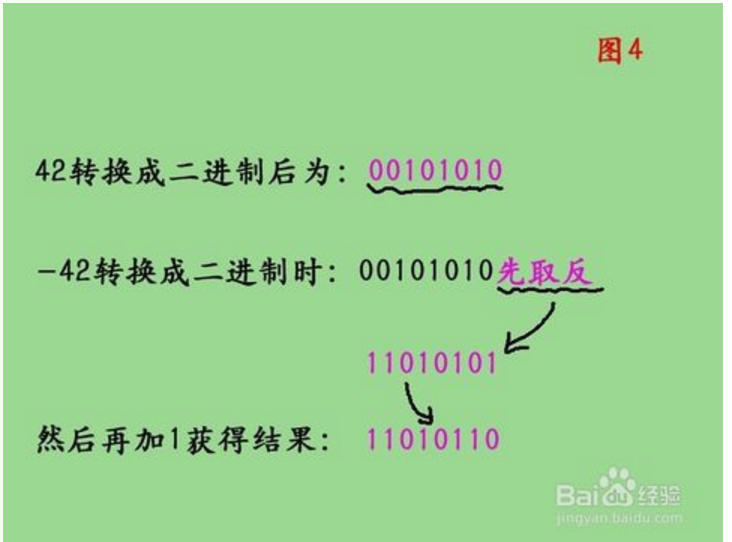
4.2、 負整數轉換成二進制
方法:先是將對應的正整數轉換成二進制後,對二進制取反,然後對結果再加一。還以42為例,負整數就是-42,如圖4所示為方法解釋。最後即為:(-42)10=(11010110)2.
5.小數轉換為二進制的方法:對小數點以後的數乘以2,有一個結果吧,取結果的整數部分(不是1就是0喽),然後再用小數部分再乘以2,再取結果的整數部分……以此類推,直到小數部分為0或者位數已經夠了就OK了。然後把取的整數部分按先後次序排列就OK了,就構成了二進制小數部分的序列,舉個例子吧,比如0.125,如圖5所示。

6.如果小數的整數部分有大於0的整數時該如何轉換呢?如以上整數轉換成二進制,小數轉換成二進制,然後加在一起就OK了,如圖6所示。

7.
整數二進制轉換為十進制:首先將二進制數補齊位數,首位如果是0就代表是正整數,如果首位是1則代表是負整數。
先看首位是0的正整數,補齊位數以後,將二進制中的位數分別將下邊對應的值相乘,然後相加得到的就為十進制,比如1010轉換為十進制,方法如圖7所示。
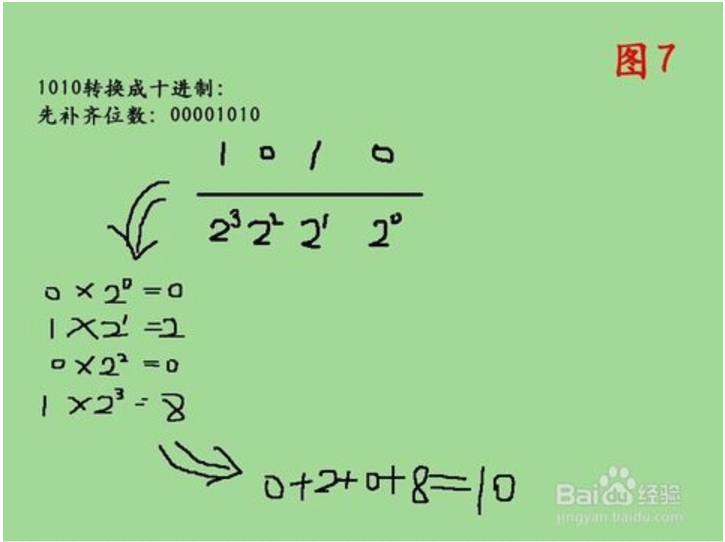
8.若二進制補足位數後首位為1時,就需要先取反再換算:例如,11101011,首位為1,那麼就先取反吧:-00010100,然後算一下10100對應的十進制為20,所以對應的十進制為-20,方法如圖8所示。

9.將有小數的二進制轉換為十進制時:例如0.1101轉換為十進制的方法:將二進制中的四位數分別於下邊(如圖9所示)對應的值相乘後相加得到的值即為換算後的十進制。
