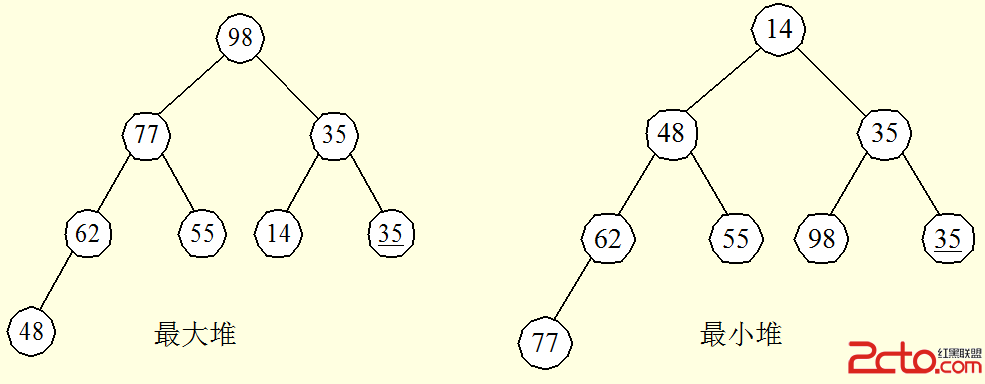
3.堆是一棵完全二叉樹。
堆有兩種:最大堆和最小堆。
最小堆中每個節點的優先級小於或者等於它的子節點;最大堆則相反,每個節點的優先級都大於或者等於它的子節點。
如下圖:
本文只著重講最大堆吧,最小堆是一樣的。
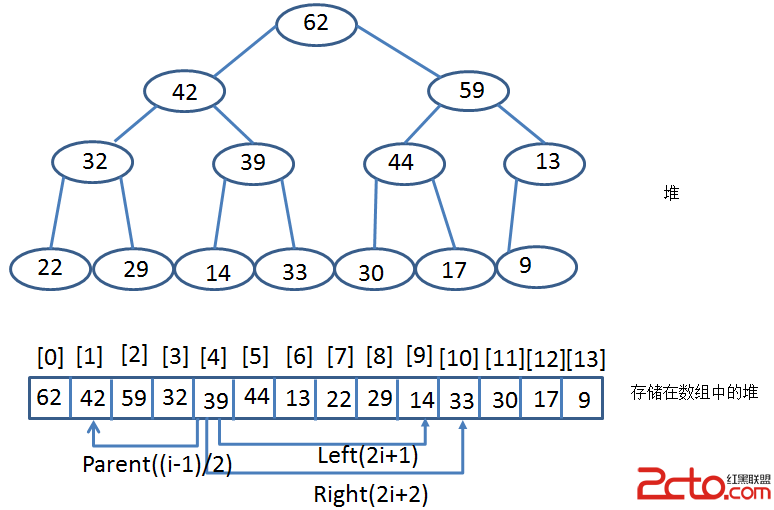
堆的大小是提前知道的,在java集合中堆是通過ArrayList數組實現的:
1.根節點位置:根節點的數據總是在數組的位置[0]
2.節點的父節點位置:假設一個非根節點的數據在數組中的位置[i],那麼它的父節點總是在位置[(i-1)/2]
3.節點的孩子節點位置:假設一個節點的數據在數組中的位置為[i],那麼它的孩子(如果有)總是在下面的這兩個位置:左孩子在[2*i+1],右孩子在[2*i+2]
在堆中主要是插入和刪除節點的操作,這兩種操作無論是哪一種,完成之後都還是一個堆,操作時要進行堆的調整,使其是個新堆。
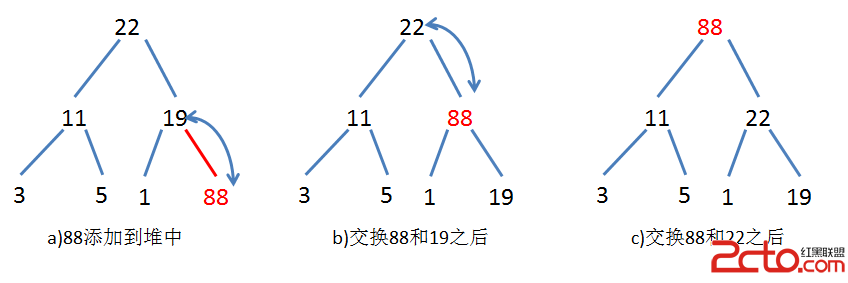
一,添加一個新節點:(不斷地和父節點比較)
插入的思路是這樣的:當插入一個元素時,先將這個元素插入到隊列尾,然後將這個新插入的元素和它的父節點進行優先權的比較,如果比父節點的優先權要大,則和父節點呼喚位置,然後再和新的父節比較,直到比新的父節點優先權小為止
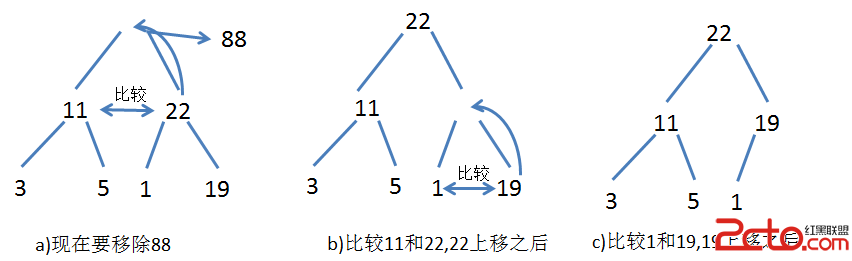
二,刪除一個節點(不斷比較左右孩子節點大小,大的上移)
從堆中刪除優先權最大的元素的思路是將隊列尾的元素值賦給根節點,隊列為賦 值為null。然後檢查新的根節點的元素優先權是否比左右子節點的元素的優先權大,如果 比左右子節點的元素的優先權小,就交換位置,重復這個過程,直到秩序正常。
heap.java實現
//最大堆 import java.util.ArrayList; public class Heap{ private ArrayList list=new ArrayList ();//用數組實現堆 public Heap(){} public Heap(E[] objects){ for(int i=0;i