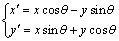平面點的旋轉公式,平面旋轉公式
定義:平面上繞它上面一點O的旋轉,是使平面上任意一對對應點P和P’與一個定點O連結的線段都相等,即|OP|=|OP’|,且有向角<POP’等於確定的有向角β,點O稱為旋轉中心,有向角β稱為旋轉角。
變換公式 取直角坐標系,以原點O為旋轉中心,旋轉角為β,平面上任意一點P(x,y)旋轉到P'(x',y')
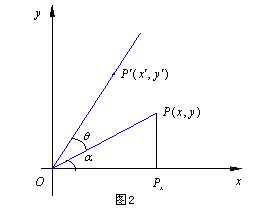
旋轉變換公式為
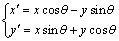

![]()
1 /// 點的旋轉
2 PointF rotatePoint(PointF p, double RotAng)
3 {
4 // 為何/180,因為弧度和角度的換算
5 double RotAngF = (RotAng * Math.PI / 180d);
6 double SinVal = (Math.Sin(RotAngF));
7 double CosVal = (Math.Cos(RotAngF));
8 double Nx = (p.X * CosVal - p.Y * SinVal);
9 double Ny = (p.Y * CosVal + p.X * SinVal);
10 return new PointF(Nx, Ny);
11 }
點的旋轉
作者:orange1438
出處:http://www.cnblogs.com/orange1438/
本文版權歸作者和博客園共有,歡迎轉載,但未經作者同意必須保留此段聲明,且在文章頁面明顯位置給出原文連接,否則保留追究法律責任的權利。