x01.Weiqi.11: 神來之筆，神來之筆的意思

x01.Weiqi.11: 神來之筆，神來之筆的意思

在圍棋中，一子兩用，可謂妙手，而一子三用，則可稱之為神來之筆。在解決征子問題時，一不小心，也來了個神來之筆，其代碼如下：

        // 征子判斷，p1, p2 為氣，p2 為前進方向，p 為逃跑之子。
        bool CanLevy(Pos p1, Pos p2, Pos p, bool isBlack = true)
        {
            if (!IsCusp(p1, p2)) return true;
            if (p == m_InvalidPos) return true;

            List<Pos> selfPoses = isBlack ? BlackPoses : WhitePoses;
            List<Pos> otherPoses = !isBlack ? BlackPoses : WhitePoses;

            // 征而被叫，豈不大笑？
            var p1_links = LinkPoses(p1).Intersect(otherPoses).ToList();
            if (p1_links.Count == 1 && p1_links.Intersect(EmptyPoses).Count() == 2)
                return false;
            var p2_links = LinkPoses(p2).Intersect(otherPoses).ToList();
            if (p2_links.Count == 1 && p2_links.Intersect(EmptyPoses).Count() == 2)
                return false;

            int count = 0;
            while (true) {
                if (!InRange(p2.Row, p2.Col))
                    break;
                bool isRow = p2.Row - p.Row == 0 ? true : false;
                int rowOffset = isRow ? (count == 0 ? p1.Row - p2.Row : p2.Row - p1.Row) : 0;
                int colOffset = isRow ? 0 : (count ==  0 ? p1.Col - p2.Col :p2.Col - p1.Col);
                Pos pos = new Pos(p2.Row + rowOffset, p2.Col + colOffset);
                var rounds = count < 5 ? LinkPoses(pos) : RoundTwoPoses(pos);
                foreach (var r in rounds) {
                    if (isBlack && count < 2) continue; // 黑需先走兩步
                    if (selfPoses.Contains(r))
                        return false;
                    if (otherPoses.Contains(r)) {
                        return true;
                    }
                }
                count++;
                p1 = p;
                p = p2;
                p2 = pos;
            }

            return true;
        }

其中，count 變量，分別控制符號轉換（count == 0），排除舊有（count < 5），黑棋預走（count < 2) 三種情況，並且三種情況皆不可少。

現在可以看看效果圖了：

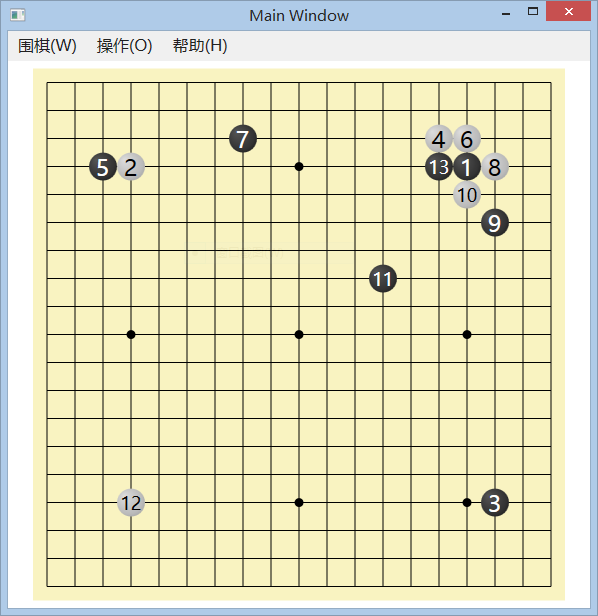
當 白10 征子時，不可逃，電腦選擇了 黑11，而 白12 時，可以逃了，電腦就聰明的選擇了 黑13，堪稱完美！

完整代碼下載，可參看上一篇博客。