程式師世界 >> 編程語言 >> .NET網頁編程 >> C# >> C#入門知識 >> PageRank 計算博客園用戶排名，pagerank博客

PageRank 計算博客園用戶排名，pagerank博客

編輯：C#入門知識

PageRank 計算博客園用戶排名，pagerank博客

PageRank 通過網頁與網頁之間的鏈接關系計算各網頁權重，一般權重高的網頁特點是：鏈接向它的網頁數量多、鏈向它的網頁其權重也較高。PageRank 就是通過這樣的連接關系，一輪輪迭代計算後得出各網頁的權重。

思路拓展一下，其實人與人之間也是連接著的，在社會的人際關系網中，每個人的社會地位和身價也是不同的。以微博為例，我們都有關注者和粉絲（類似網頁之間的鏈接），可以發現所謂的“大V”基本上粉絲數量多，並且粉絲裡不乏很多其他“大V”，所以這個帳號的價值就大。

同樣博客園也具有類似的社交關系，用戶可以選擇“關注的人”以及“關注我的人”，理論上是可以用 PageRank 算法算出哪些用戶更受大家歡迎，於是本文代大家八卦了一下，文章較長，只想看排名的同學請直接拉到末尾。。。

PageRank 算法簡介

1. 數學模型

《數學之美》第10章的延伸閱讀部分，對 PageRank 的計算方法進行了簡單介紹，但原書有些錯誤，修改後描述如下：

我們設向量 B 為第一、第二…第N個網頁的網頁排名

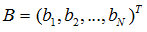
矩陣 A 代表網頁之間的權重輸出關系，其中 a_mn 代表第 m 個網頁向第 n 個網頁的輸出權重。

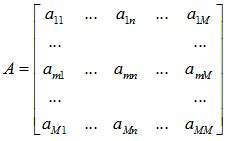
輸出權重計算較為簡單：假設 m 一共有10個出鏈，指向 n 的一共有2個，那麼 m 向 n 輸出的權重就為 2/10。

現在問題變為：A 是已知的，我們要通過計算得到 B。

假設 B_i 是第 i 次迭代的結果，那麼

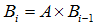
初始假設所有網頁的排名都是 1/N （N為網頁總數量），即

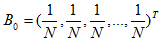
通過上述迭代計算，最終 B_i 會收斂，即 B_i 無限趨近於 B，此時 B = B × A。

2. 具體示例

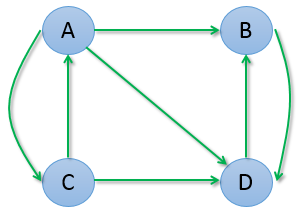
假設有網頁A、B、C、D，它們之間的鏈接關系如下圖所示

計算 B₁ 如下：

不斷迭代，計算結果如下：

第 1次迭代: 0.125, 0.333, 0.083, 0.458
第 2次迭代: 0.042, 0.500, 0.042, 0.417
第 3次迭代: 0.021, 0.431, 0.014, 0.535
第 4次迭代: 0.007, 0.542, 0.007, 0.444
第 5次迭代: 0.003, 0.447, 0.002, 0.547
第 6次迭代: 0.001, 0.549, 0.001, 0.449
第 7次迭代: 0.001, 0.449, 0.000, 0.550
第 8次迭代: 0.000, 0.550, 0.000, 0.450
第 9次迭代: 0.000, 0.450, 0.000, 0.550
第10次迭代: 0.000, 0.550, 0.000, 0.450
... ...

我們可以發現，A 和 C 的權重變為0，而 B 和 D 的權重也趨於在 0.5 附近擺動。從圖中也可以觀察出：A 和 C 之間有互相鏈接，但它們又把權重輸出給了 B 和 D，而 B 和 D之間互相鏈接，並不向 A 或 C 輸出任何權重，所以久而久之權重就都轉移到 B 和 D 了。

PageRank 的改進

上面是最簡單正常的情況，考慮一下兩種特殊情況：

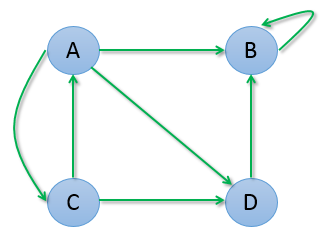
第一種情況是，B 存在導向自己的鏈接，迭代計算過程是：

第 1次迭代: 0.125, 0.583, 0.083, 0.208
第 2次迭代: 0.042, 0.833, 0.042, 0.083
第 3次迭代: 0.021, 0.931, 0.014, 0.035
第 4次迭代: 0.007, 0.972, 0.007, 0.014
第 5次迭代: 0.003, 0.988, 0.002, 0.006
第 6次迭代: 0.001, 0.995, 0.001, 0.002
第 7次迭代: 0.001, 0.998, 0.000, 0.001
第 8次迭代: 0.000, 0.999, 0.000, 0.000
第 9次迭代: 0.000, 1.000, 0.000, 0.000
第10次迭代: 0.000, 1.000, 0.000, 0.000
... ...

我們發現最終 B 權重變為1，其它所有網頁的權重都變為了0 =。=!

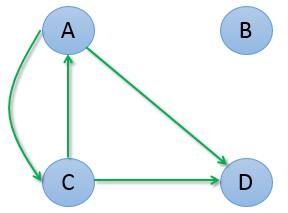
第二種情況是 B 是孤立於其它網頁的，既沒有入鏈也沒有出鏈，迭代計算過程是：

第 1次迭代: 0.125, 0.000, 0.125, 0.250
第 2次迭代: 0.063, 0.000, 0.063, 0.125
第 3次迭代: 0.031, 0.000, 0.031, 0.063
第 4次迭代: 0.016, 0.000, 0.016, 0.031
第 5次迭代: 0.008, 0.000, 0.008, 0.016
第 6次迭代: 0.004, 0.000, 0.004, 0.008
第 7次迭代: 0.002, 0.000, 0.002, 0.004
第 8次迭代: 0.001, 0.000, 0.001, 0.002
第 9次迭代: 0.000, 0.000, 0.000, 0.001
第10次迭代: 0.000, 0.000, 0.000, 0.000
... ...

我們發現所有網頁權重都變為了0 =。=!

出現這種情況是因為上面的數學模型出現了問題，該模型認為上網者從一個網頁浏覽下一個網頁都是通過頁面的超鏈接。想象一下正常的上網情景，其實我們在看完一個網頁後，可能直接在浏覽器輸入一個網址，而不通過上一個頁面的超鏈接。

我們假設每個網頁被用戶通過直接訪問方式的概率是相等的，即 1/N，N 為網頁總數，設矩陣 e 如下：

設用戶通過頁面超鏈接浏覽下一網頁的概率為 α，則直接訪問的方式浏覽下一個網頁的概率為 1 - α，改進上一節的迭代公式為：

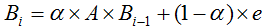
通常情況下設 α 為0.8，上一節”具體示例”的計算變為如下：

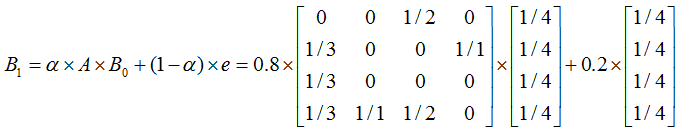
迭代過程如下：

第 1次迭代: 0.150, 0.317, 0.117, 0.417
第 2次迭代: 0.097, 0.423, 0.090, 0.390
第 3次迭代: 0.086, 0.388, 0.076, 0.450
第 4次迭代: 0.080, 0.433, 0.073, 0.413
第 5次迭代: 0.079, 0.402, 0.071, 0.447
第 6次迭代: 0.079, 0.429, 0.071, 0.421
第 7次迭代: 0.078, 0.408, 0.071, 0.443
第 8次迭代: 0.078, 0.425, 0.071, 0.426
第 9次迭代: 0.078, 0.412, 0.071, 0.439
第10次迭代: 0.078, 0.422, 0.071, 0.428
第11次迭代: 0.078, 0.414, 0.071, 0.437
第12次迭代: 0.078, 0.421, 0.071, 0.430
第13次迭代: 0.078, 0.415, 0.071, 0.436
第14次迭代: 0.078, 0.419, 0.071, 0.431
第15次迭代: 0.078, 0.416, 0.071, 0.435
第16次迭代: 0.078, 0.419, 0.071, 0.432
第17次迭代: 0.078, 0.416, 0.071, 0.434
第18次迭代: 0.078, 0.418, 0.071, 0.432
第19次迭代: 0.078, 0.417, 0.071, 0.434
第20次迭代: 0.078, 0.418, 0.071, 0.433
... ...

PageRank 算法實現

互聯網的網頁數量是 Billion 級別的，所以不可能一下子初始化矩陣 A ，試想一下 10億 × 10億的矩陣是什麼概念！

這時就用到稀疏矩陣了，定義稀疏矩陣的結構如下（其實是稀疏矩陣的一行）：

public class SparseMatrix<T>
{
    public SparseMatrix(T head, double rank)
    {
        Head = head;
        LinkedItems = new List<T>();
        Rank = rank;
    }

    /// <summary>
    ///     稀疏矩陣頭
    /// </summary>
    public T Head { get; private set; }

    public double Rank { get; set; }

    /// <summary>
    ///     稀疏矩陣鏈接的項目
    /// </summary>
    public List<T> LinkedItems { get; set; }

    public void AddLink(T linkedItem)
    {
        LinkedItems.Add(linkedItem);
    }
}

第一節中的鏈接示例圖，就可以用如下代碼表示：

Dictionary<char, SparseMatrix<char>> matrix = new Dictionary<char, SparseMatrix<char>> 
{
    {'A', new SparseMatrix<char>('A', 0.25){LinkedItems = new List<char>{'B', 'C', 'D'}}},
    {'B', new SparseMatrix<char>('B', 0.25){LinkedItems = new List<char>{'D'}}},
    {'C', new SparseMatrix<char>('C', 0.25){LinkedItems = new List<char>{'A', 'D'}}},
    {'D', new SparseMatrix<char>('D', 0.25){LinkedItems = new List<char>{'B'}}}
};

通過稀疏矩陣計算，與原先的整個矩陣行列式計算有較大不同，計算次序已經發生了變化。原先矩陣是一行乘以權重的豎列，稀疏矩陣則變為類似於按原先矩陣的豎列與權重相乘。矩陣運算中當然不允許 1 × N 矩陣與 1 × N 矩陣相乘的情況，我們能做的就是先將一項項算好，比如先算 A 這一行，算出 A 給 B、C、D輸出多少權重，在一個類似字典類型的數據結構裡，給 B、C和 D 各加上一筆，像是一個 Map-Reduce 過程。

public class MapReduce<T>
{
    private readonly Dictionary<T, double> _map;

    public MapReduce()
    {
        _map = new Dictionary<T, double>();
    }

    public double Reduce(T key, double value)
    {
        if (_map.ContainsKey(key))
        {
            _map[key] += value;
            return _map[key];
        }
        _map.Add(key, value);
        return value;
    }

    public double GetOrSetDefaultValue(T key)
    {
        if (_map.ContainsKey(key))
            return _map[key];
        _map.Add(key, 0.0);
        return 0.0;
    }
}

PageRank 設計如下：

public class PageRank<T>
{
    private MapReduce<T> _mapReduce;
    private readonly double _stayProbability;
    private readonly double _averageRank;

    /// <summary>
    /// 
    /// </summary>
    /// <param name="totalCount">項目總數</param>
    /// <param name="stayProbability">保持留在某個項目, 不跳轉的概率</param>
    public PageRank(int totalCount, double stayProbability = 0.8)
    {
        _mapReduce = new MapReduce<T>();
        _stayProbability = stayProbability;
        _averageRank = 1.0 / totalCount;
    }

    /// <summary>
    ///     計算下一輪PageRank
    /// </summary>
    public void NextCircle()
    {
        _mapReduce = new MapReduce<T>();
    }

    /// <summary>
    ///     計算一條行列式
    /// </summary>
    /// <param name="sparseMatrix">稀疏矩陣</param>
    public void Calc(SparseMatrix<T> sparseMatrix)
    {
        var outputRank = 1.0 / sparseMatrix.LinkedItems.Count;

        foreach (var item in sparseMatrix.LinkedItems)
        {
            _mapReduce.Reduce(item,
                _stayProbability * outputRank * sparseMatrix.Rank);
        }
        //當沒有其它鏈接指向Head的時候, 以防漏項
        _mapReduce.Reduce(sparseMatrix.Head, (1 - _stayProbability) * _averageRank);
    }

    /// <summary>
    ///     一輪PageRank迭代之後, 獲取最新的PageRank並更新
    /// </summary>
    /// <param name="key"></param>
    /// <returns></returns>
    public double GetCurrentRank(T key)
    {
        return _mapReduce.GetOrSetDefaultValue(key);
    }
}

調用示例：

var matrix = new Dictionary<char, SparseMatrix<char>> 
{
    {'A', new SparseMatrix<char>('A', 0.25){LinkedItems = new List<char>{'B', 'C', 'D'}}},
    {'B', new SparseMatrix<char>('B', 0.25){LinkedItems = new List<char>{'D'}}},
    {'C', new SparseMatrix<char>('C', 0.25){LinkedItems = new List<char>{'A', 'D'}}},
    {'D', new SparseMatrix<char>('D', 0.25){LinkedItems = new List<char>{'B'}}}
};

var pageRank = new PageRank<char>(matrix.Count);
//計算30輪
for (int i = 1; i <= 30; i++)
{
    pageRank.NextCircle();
    foreach (var item in matrix)
    {
        pageRank.Calc(item.Value);
    }
    foreach (var item in matrix)
    {
        var cRank = pageRank.GetCurrentRank(item.Key);
        item.Value.Rank = cRank;
    }
    var str = string.Join(", ", matrix.Select(item => item.Value.Rank.ToString("N3")));
    Console.WriteLine(string.Format("第{0,2}次迭代: {1}", i, str));
}

開源地址：https://github.com/CreateChen/PageRank

博客園用戶權重計算

寫一個簡單的網絡爬蟲，爬取博客園所有用戶的 Id、關注的人等信息（過程略），最終得到如下結構的表格：

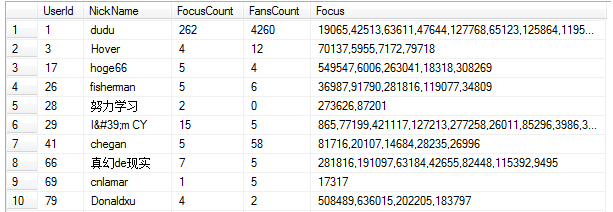
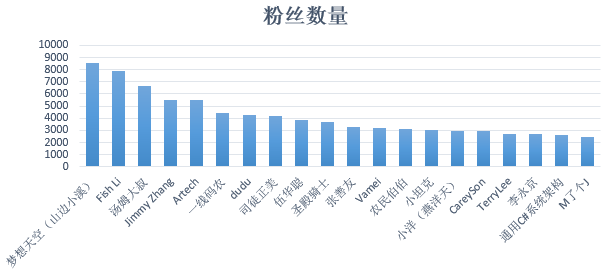
首先八卦一下粉絲數量 Top 20，方便與 PageRank 算出的結果做對比。

下面進入真正的 PageRank 計算了，利用第二節的程序計算，一次迭代計算速度很快，從數據庫獲取數據並且計算完畢只要6秒，更新數據庫的 Rank 字段需要近30秒。下表展示的是第1輪迭代、第15輪的用戶的權重：

排名 NickName Rank … NickName Rank 1 夢想天空（山邊小溪） 0.002165 … 夢想天空（山邊小溪） 0.001346 2 Fish Li 0.00192 … dudu 0.001334 3 湯姆大叔 0.001514 … Artech 0.00102 4 Jimmy Zhang 0.001281 … Fish Li 0.000947 5 M了個J 0.001244 … 司徒正美 0.000786 6 Artech 0.001164 … 李永京 0.000746 7 農民伯伯 0.001161 … 湯姆大叔 0.0007 8 司徒正美 0.000987 … 趣味蘋果開發 0.000677 9 Vamei 0.000953 … 通用C#系統架構 0.000601 10 tornadomeet 0.000858 … M了個J 0.00059 11 伍華聰 0.000787 … Jimmy Zhang 0.000586 12 一線碼農 0.000786 … banban 0.000576 13 吳秦 0.00075 … Milo Yip 0.000532 14 dudu 0.000729 … 張善友 0.000488 15 蟲師 0.000722 … Jeffrey Zhao 0.00047 16 小坦克 0.000691 … 覺先 0.000462 17 Rollen Holt 0.000649 … SoftwareTeacher 0.000444 18 聖殿騎士 0.000545 … 博客園團隊 0.000434 19 CareySon 0.000538 … TerryLee 0.000434 20 文頂頂 0.000538 … 胡尐睿丶 0.00043 21 小洋（燕洋天） 0.000535 … T2噬菌體 0.000422 22 蝦皮 0.000529 … 農民伯伯 0.000415 23 JerryLead 0.000526 … Anytao 0.000411 24 李永京 0.000508 … 聖殿騎士 0.000411 25 方倍工作室 0.000505 … 深藍色右手 0.000406 26 cloudgamer 0.000486 … 伍華聰 0.0004 27 楊中科 0.000483 … 一線碼農 0.000399 28 TerryLee 0.000467 … 小洋（燕洋天） 0.000388 29 張善友 0.000466 … Cat Chen 0.000374 30 深藍色右手 0.000457 … CareySon 0.000371 31 謙虛的天下 0.000445 … Vamei 0.000365 32 通用C#系統架構 0.000435 … ziqiu.zhang 0.000358 33 胡尐睿丶 0.00042 … 周金根 0.000351 34 三生石上 0.000413 … 伍迷 0.000342 35 KenshinCui 0.000397 … xiaotie 0.000332 36 博客園團隊 0.000389 … 謙虛的天下 0.000331 37 酸奶小妹 0.000387 … 冠軍 0.000329 38 Milo Yip 0.000372 … 吳秦 0.000327 39 伍迷 0.00037 … cloudgamer 0.000318 40 子龍山人 0.000369 … tornadomeet 0.000305 41 Insus.NET 0.000369 … 酸奶小妹 0.0003 42 菩提樹下的楊過 0.000369 … 小坦克 0.0003 43 萬一 0.000368 … 【當耐特】 0.000285 44 _Luc_ 0.000367 … chenkai 0.000277 45 夏天的森林 0.000354 … Justin 0.000274 46 ziqiu.zhang 0.000351 … 裝配腦袋 0.000272 47 Jeffrey Zhao 0.000351 … 蟲師 0.000271 48 葉小钗 0.000343 … 菩提樹下的楊過 0.000271 49 真 OO無雙 0.000343 … Gnie 0.00027 50 SoftwareTeacher 0.000337 … 張逸 0.000252 51 webabcd 0.000333 … LeftNotEasy 0.000245 52 T2噬菌體 0.000331 … 小靜（Cathy） 0.00024 53 Ruthless 0.000328 … Gray Zhang 0.000237 54 peida 0.000327 … Jesse Liu 0.000237 55 陳梓瀚(vczh) 0.000324 … JerryLead 0.000231 56 聶微東 0.000322 … webabcd 0.000228 57 Jesse Liu 0.000317 … fly in ocean 0.000225 58 【當耐特】 0.000288 … Anders Cui 0.000221 59 西西吹雪 0.000286 … 代震軍 0.000221 60 snandy 0.000286 … COM張 0.00022 61 Phinecos(洞庭散人) 0.000286 … 楠小楠 0.00021 62 David_Tang 0.000283 … 何戈洲 0.00021 63 yangecnu 0.000282 … 三生石上 0.000207 64 孤傲蒼狼 0.000278 … 路過秋天 0.000204 65 Learning hard 0.000277 … Jake Lin 0.000203 66 Stephen_Liu 0.000272 … 飛洋過海 0.000201 67 Terry_龍 0.000269 … 陳希章 0.0002 68 xiaotie 0.000269 … 葉小钗 0.000198 69 Leo Chin 0.000269 … eaglet 0.000197 70 海子 0.000267 … 陳梓瀚(vczh) 0.000197 71 Barret Lee 0.000264 … _Luc_ 0.000194 72 路過秋天 0.000263 … snandy 0.000191 73 Dsp Tian 0.000255 … 新瓶老酒 0.000186 74 Devin Zhang 0.000255 … Bēniaǒ 0.000185 75 蒼梧 0.000252 … dax.net 0.000185 76 覺先 0.000251 … 麒麟.NET 0.000185 77 周金根 0.00025 … 方倍工作室 0.000183 78 冠軍 0.000249 … 萬一 0.000181 79 何戈洲 0.000242 … 陳碩 0.000179 80 劉冬.NET 0.000237 … 任力 0.000177 81 hoojo 0.000236 … Franky 0.000177 82 Orisun 0.000236 … 蝦皮 0.000173 83 CrazyBingo 0.000235 … Stephen_Liu 0.000172 84 代震軍 0.000234 … 石破天驚 0.000172 85 minglz 0.000231 … 岑安 0.000171 86 Alexia(minmin) 0.000226 … 楊中科 0.00017 87 Gnie 0.000226 … iOS之旅 0.00017 88 鄒華棟 0.000225 … 橫刀天笑 0.000169 89 Samaritans 0.000224 … 邀月 0.000168 90 Aaron艾倫 0.000222 … jv9 0.000165 91 邀月 0.000221 … 聶微東 0.000164 92 Healtheon 0.000219 … 創想中國(羲聞) 0.000164 93 李林峰的園子 0.000219 … CoderZh 0.000163 94 呂震宇 0.000218 … Luminji 0.000163 95 沈逸 0.000218 … winter-cn 0.000163 96 LeftNotEasy 0.000213 … Rollen Holt 0.000161 97 陳希章 0.000212 … 金色海洋（jyk）陽光男孩 0.000159 98 Hongten 0.000211 … 重典 0.000159 99 創想中國(羲聞) 0.000211 … 阿一(楊正祎) 0.000157 100 Cat Chen 0.000208 … 夜裡的煙 0.000157

如果你對完整的計算過程感興趣，可以下載完整表格。想了解自己的權重及排名請在下方留言。

當然在實際計算排名過程中，不單單依據粉絲與關注者之間的關系，還需要結合文章的質量、更新頻率及數量，最後給一個綜合的評分。總之：被關注數量越多、經常寫文章、文章被贊的次數越多、評論次數多，就越能提升社區影響力。

本文鏈接：http://www.cnblogs.com/technology/p/PageRank.html