遇到一個想做的功能,但是實現不了,核心原因是因為對U3D的3D數學概念沒有靈活吃透。故再次系統學習之—第三次學習3D數學.
本次,希望實現的功能很簡單:
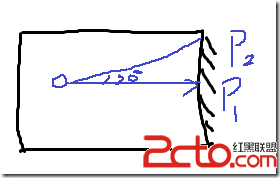
如在小地圖中,希望可以動態畫出Player當前的位置、z的朝向:用3條線、z軸正向、30°旋轉、-30°旋轉。
問題是:0點可以獲得,P1點? P2點是未知的。
我嘗試了2個小時,結果不竟如人意,少於沮喪。

不得不,再次花點時間系統的學習3D數學:
做個游戲,列表出你用過的Vector3的API,分析分析用到的Vector3是向量(V)還是點(P)
需求
API
向量(V)
點(P)
備注
平滑位移
Vector3 MoveTowards(Vector3 current, Vector3 target, float maxDistanceDelta);
P
平滑位移
Vector3 Slerp(Vector3 from, Vector3 to, float t)
P
新的坐標點
this.m_transform.position = pos;
P
符合常規思維
變動一次坐標
m_transform.Translate(new Vector3(rx, 0, -m_Speed * Time.deltaTime));
V
可認為是增量求方向
Vector3 relativePos = this.m_transform.position – m_Player.position;
V
向量減法,較難理解設置新坐標點
lineRenderer.SetPosition(0,this.gameObject.transform.position);
m_NavAgent.SetDestination(this.m_Player.transform.position);
P
符合常規思維
新的位置
pointer.transform.position = hitInfo.point + (transform.position – hitInfo.point) * 0.01f;
P、V
力的疊加?
求距離
float dis = Vector3.Distance(v1, v2);
float f1 = (v1 – v2).sqrMagnitude;
float f3 = (v1 – v2).magnitude;
P、V
Distance用點即可
向量減法也可以
縮放正向
Vector3 v3 = this.m_transform.forward * 200f;
V
V的數乘
射線檢測
Ray r = new Ray(source, dest);
Physics.Raycast(r, out hit, 1000, m_ShootMask)
V、P
Source:P
Dest:V
加一個力
rigidbody.AddForce (0, 10, 0);
V
依據這個游戲,可以整理出目前用到的有4個組件(含Vector 3)會發生位移:
位移常用的4個組件和Vector3:
組件
函數
Unity 聖典的API說明
是否
用過
transform組件
translate函數
向某方向移動物體多少距離【默認local坐標系】
或者相對某物體移動
yes
Position屬性
在世界空間坐標transform的位置
Yes
RigidBody組件
[FixedUpdate函數]
Velocity屬性
剛體的速度向量
Unity 官方demo Done用的很酷
Yes
AddForce函數
添加一個力到剛體。作為結果剛體將開始移動。
yes
MovePosition函數
移動剛體到position
NavMeshAgent組件
SetDestination函數
設置自動Path目標點
yes
CharacterController
組件
Move函數
一個更加復雜的運動函數,每次都絕對運動
yes
SimpleMove函數
以一定的速度移動角色
Vector3向量
Lerp函數
兩個向量之間的線性插值。
“像彈簧一個跟隨目標物體”
Slerp函數
球形插值在兩個向量之間
“在日出和日落之間動畫弧線”
MoveToward函數
當前的地點移向目標
和Vector3.Lerp相同,maxDistanceDelta限速
SmoothDamp 函數
隨著時間的推移,逐漸改變一個向量朝向預期的目標。
我的幾個向量相關的問題:
如何判斷A向量和B向量是否同方向? 如何判斷A向量和B向量前、後、左、右? 如何判斷A向量和B向量的夾角? 向量的減法貌似比加法更有用一些? Vector.Forward和this.transform.Forward都表達local坐標系,那麼數值為什麼不一樣呢?
旋轉在3D中是比較復雜的,在Unity 3D中一般用Quaternion來進行旋轉, 旋轉僅涉及向量的概念(向量的方向),請思考對於坐標點或者零向量旋轉有無意義?
而按照Unity 3D API官方的說法,僅有約7個方法或者操作符比較常用,且占99%的概率,我截止目前還沒有用到這麼多,我用到的Quaterniong約有4個函數。
旋轉常用7個API:
Quaternion API
Unity 聖典的API說明
是否
用過
Quaternion.LookRotation
創建一個旋轉,沿著forward(z軸)並且頭部沿著upwards(y軸)的約束注視。也就是建立一個旋轉,使z軸朝向y軸朝向up。 常用的是transform.LookAt
yes
Quaternion.Angle
返回a和b兩者之間的角度。
Quaternion.Euler
返回一個旋轉角度,繞z軸旋轉z度,繞x軸旋轉x度,繞y軸旋轉y度(像這樣的順序)。
yes
Quaternion.Slerp
球形插值,通過t值from向to之間插值。
Quaternion.FromToRotation
從fromDirection到toDirection創建一個旋轉。
Quaternion.identity
返回恆等式旋轉(只讀)。這個四元數對於“無旋轉”:這個物體完全對齊於世界或父軸。
yes
Quaternion.operator *
由另一個四元數來旋轉一個旋轉角度,或由一個旋轉角度來旋轉一個向量
yes
我的幾個旋轉相關的問題:
1 Quaternion.LookRotation和Vector3.RotateTowards的區別?
2 Quaternion.Angle和Vector3.Angle的區別?
3 Quaternion.LookRotation和transform.LookAt的區別?
[官方回答: 大多數時間你可以使用transform.LookAt代替
Quaternion.LookRotation]
4 如何實現2個GameObject face to face,即Z軸相對?
磨刀不誤砍柴工: 經過一周的復習、反復驗證,果然在系統學習3D 數學後,要實現的功能可以了,如下:
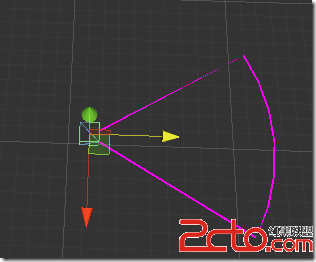
總結:
據說80%、90%Unity 3D程序員是自學的,大多數是看看書、實戰視頻、源碼分析;而科班出生的同學會有3D數學這門核心課–估計占一個學期、會有作業等。為了趕上科班同學的水平,花點時間,補補數學知識,會使得自己少走一些彎路。一句話:”3D數學模型很關鍵。“