C#語言支持表B-1所示的11種數值類型,分別為整數,浮點數和小數。
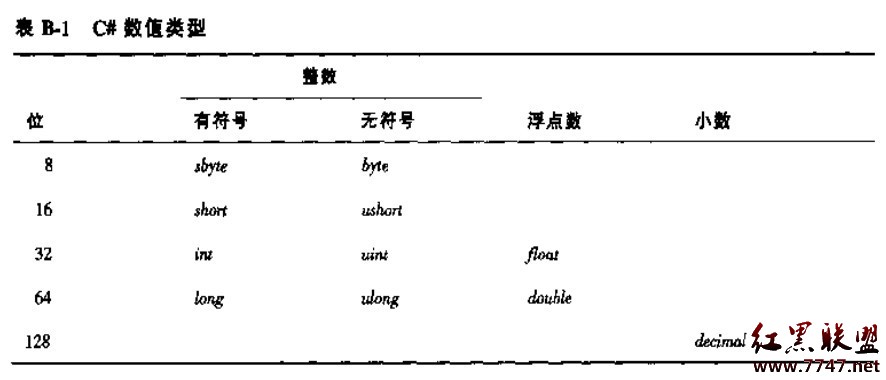
在一個c#程序中,整數(沒有小數點的數)被認為是一個int類型(除非其值大於最大的int值),根據數據值,該數據依次被視為uint,long,ulong,帶小數點的數被認為是一個double值。這就是說(1.0).GetType()==typeof(double).
你可以在數字說明上使用前綴來表明自己的意圖。

其中u代表無符號的意思。因為無符號,所以u代表了數據是正數或0,不可能是負數。
A:檢查整數溢出
考慮下面的代碼:
short s=32767;s+=1;
ushort us=0;us-=1;
在第一種情況下,一個有符號的數加1,經過其最大值,由於整數在內存中存儲方式的原因,結果是-32768.
在第二種情況下,一個無符號的數被減為小於0,結果將是65535.
在這兩道例子中,分別出現了上溢和下溢的情況,如果想避免這種情況的發生,可以使用checked關鍵字,
或者使用下面的編譯器開關:
/checked+
默認編譯器開關對應為:/checked-
如果使用checked關鍵字:
short s=32767;
checked
{
s+=1; //將產生一個OverFlowException.
}
迄今為止,我一直都在獨自介紹運行時的整數向上或向下溢出檢查,在默認情況下編譯器會將編譯時的向上和向下溢出標記為一個錯誤,而和你的編譯器開關無關。
例如語句short s=32767+1;
會產生一個編譯時錯誤,因為在編譯期間對加法進行求值.
例如下面的例子:
const int i1=65536;
const int i2=65536;
int i3=i1*i2;
因為i1,i2都是const值,所以編譯器在編譯的時候會嘗試對i3=i1*i2進行求值,並遇到一個向上溢出。所以會導致編譯錯誤。
編譯器開關不會覆蓋這一行為,但是unchecked關鍵字可以覆蓋這種行為。
int i3=unchecked(i1*i2).可以正常編譯.
B:小數類型
decimal 關鍵字表示 128 位數據類型。同浮點型相比,decimal 類型具有更高的精度和更小的范圍,這使它適合於財務和貨幣計算。decimal 類型的大致范圍和精度如下表所示。
它使用16字節(128位)存儲每一個值。128位被劃分為96位整數位,一個符號位,以及一個可以在0~28之間變化的比例因子。在數學上,這個比例因子是一個10的負指數冪,表示數值中小數點位置的編號。
例如,如果一個小數定義等於12.34,那麼這個數的存儲方式是整數0x4D2(或1234),以及一個比例因子2,
只要一個小數具有(或小於)28個有效數字以及(或小於)28個小數位置,decimal數據類型就可以准確的存儲它。對於浮點數而言,這是不成立的!,如果定義一個float值等於12.34,那麼它會被存儲為0xC570A4(或12939428)除以0x100000(或1048576),這個值等於12.340000152587890625 約等於12.34。即使您將一個double值定義為等於12.34,它也是被存儲為:0x18AE147AE147AE(或6 946 802 425 218 990)除以0x2000000(或562 949 953 421 312),它也只是約等於12.34.
這就是你在不想讓美分神秘的出現和消失的地方執行計算時應該使用decimal的原因,因為浮點數不精確。
浮點數據類型在科學和工程應用方面很合適,但不是金融應用所期望的。
Decimal的構造函數(節選)
Decimal(int iLow,int iMiddle,int iHigh,bool bNegative,byte byScale)
例如表達式:new Decimal(123456789,0,0,false,5)
創建了一個decimal類型的小數:1234.56789.,
5代表小數點從左邊開始往右邊開始算。移動5位。
如果最後一個參數為1,則為12345678.9.
最後一個參數為2,則為1234567.89.
最後一個參數為3,則為123456.789
...
小數正值的最大值是:new Decimal(-1,-1,-1,false,0) ==Decimal.MaxValue.
接近0的最小Decimal值是:new Decimal(1,0,0,false,28)==0.0000000000000000000000000001==1*10-28.
如果在C#程序中將這個數除以2,那麼結果將是0.
在上面我已經指出浮點表示法為什麼經常是近似值。當你開始在浮點數上執行算術運算時,近似情況可能更嚴重。
例如,幾乎每一個使用浮點數的人都很清楚的知道,應該存儲為4.55的數經常被存儲為4.549999或4.550001.
小數表示的情況要好很多,例如假設m1被定義為
decimal m1=12.34
在內部m1有一個整數部分1234和一個比例因子2,同時假設m2被定義為
decimal m2=56.789;
整數部分是56789,比例因子為3,現在將兩個數相加:
decimal m3=m1+m2;
在內部,m1的整數部分被乘以10(得到12340),比例因子被設置為3.現在整數部分直接相加:12340+56789等於69129,比例因子為3,實際值是69.129.每一個數都是准確的。
現在將這兩個數相乘:
decimal m4=m1*m2;
在內部,兩個整數部分相乘(1234*56789等於70 077 626),比例因子相加(2+3等於5)。實際的數值結果為:70.077626。這一次,計算也是准確的。
在相除時....哦,My god,除法是雜亂的,無論你怎樣去做都是如此,但是對於大多數情況而言,使用Decimal你可以更好的控制結果的精度和准確度.