根據這道題目的意思,我們可以建一張圖,對於兩個booked taxi ride,ri和rj如果一輛車能夠先完成ri的任務再有時間趕去完成rj的任務,那麼就建立一條ri指向rj的邊。
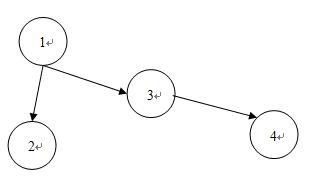
按照題目的要求,要選擇最少的taxi來完成這些任務。顯然在上面這個例子中,需要安排2輛taxi。結合這個圖,可以把題目的要求轉化為找出最少的路徑條數,使得這些路徑覆蓋途中所有的邊,例如可以選擇2條路徑1->3->4和1->2就可以覆蓋所有的邊。也可以選擇1->3->4和2(因為2作為初始站,不需要由1轉移過來)。對於一條連續的路徑vi1->vi2->…vik由於這條路徑上的任務實際上是由一輛taxi來完成的,可以吧這條路徑退化成兩個點vi1->vik。有了這兩步建圖的步驟以後,問題的求解就可以變為找出頂點集的一個最小子集,使這個頂點子集覆蓋所有的邊(每條邊都至少和一個頂點集的頂點相連)。這個問題就是圖的最小點覆蓋。再看這張圖,還有一些性質能夠讓我們更好地求出最小點覆蓋。這個圖是一個有向無環圖,沒有自環,就可以拆點,把原先建的圖變成一張二分圖。
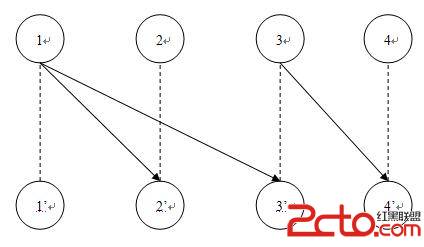
可以再圖中看出,上面舉出的一條路徑1->3->4對應了這個二分圖中的路徑1->3’->3->4’,在這個二分圖中就需要求一個最大獨立子集(這裡的4點就是一條路徑的終點,沒一條路徑即對應有一個終點!)。二分圖的最大獨立數是總點數與最大匹配數的差值。接下來建圖,拆點,求二分圖最大匹配就能解決這道題目了。
首先輸入一個時間,為一輛汽車開車的時候對應的時間,然後是起點(x1,y1),再是終點(x2,y2),起點到終點的時間為|x1-x2|+|y1-y2|,假如開始的時間加上途中經歷過的時間加上第一輛車得終點到第二輛車的起點的時間小於第二輛車起始的時間,那就得不要多派出一輛車
[csharp]
#include"stdio.h"
#include"string.h"
#include"stdlib.h"
#include"math.h"
int map[501][501],mark[501],link[501],v[501];
int n,m;
char time[10];
struct node
{
int x1,x2,y1,y2;
int t,sum;
}aa[501];
int fun(int x1,int y1,int x2,int y2)
{
return abs(x1-x2)+abs(y1-y2);
}
int dfs(int k)
{
int i;
for(i=0;i<m;i++)
{
if(map[k][i]&&!v[i])
{
v[i]=1;
if(link[i]==-1||dfs(link[i]))
{
link[i]=k;
return 1;
}
}
}
return 0;
}
int main()
{
int i,j,ans;
scanf("%d",&n);
while(n--)
{
scanf("%d",&m);
for(i=0;i<m;i++)
{
scanf("%s",time);
scanf("%d%d%d%d",&aa[i].x1,&aa[i].y1,&aa[i].x2,&aa[i].y2);
aa[i].t=(time[0]-'0')*10*60+(time[1]-'0')*60
+(time[3]-'0')*10+(time[4]-'0');
aa[i].sum=fun(aa[i].x1,aa[i].y1,aa[i].x2,aa[i].y2);
}
memset(map,0,sizeof(map));
for(i=0;i<m-1;i++)
{
for(j=i+1;j<m;j++)
{
if((aa[i].t+aa[i].sum+fun(aa[i].x2,aa[i].y2,aa[j].x1,aa[j].y1))<aa[j].t)
map[i][j]=1;
}
}
ans=0;
memset(link,-1,sizeof(link));
for(i=0;i<m;i++)
{
memset(v,0,sizeof(v));
ans+=dfs(i);
}
printf("%d\n",m-ans);
}
return 0;
}
作者:yyf573462811