摘要：任務指派問題是典型的組合優化問題，得到了廣泛的研究。基於基因表達式編程的思想，設計了任務指派問題求解的算法，並用C#實現了該算法。結合人力資源任務分配的實例進行了實驗分析和研究，獲得了人員與崗位配置的最優解。實驗表明算法設計是正確性和有效性，因而為企業人員安排提供參考依據。
關鍵詞：TAP問題；基因表達式編程；逆串算子
中圖分類號: TP301.6 文獻標識碼: A
The Design and Implementation of Task Assigned ProblemBased on Gene Expression Programming
ZHU Ming-fang1,2, Ye Fei-yue1,2,PAN Yu1,2 , DING Xiao-wei2,
(1. KeyLaboratory of Cloud Computing & Intelligent Information Processing ofChangzhou City, Jiangsu Teachers University of Technology, Changzhou, 213001,China；
(2. 2. School of Computer Engineering, Jiangsu Teachers Universityof Technology, Changzhou， 213001,China)
Abstract: Task assignmentproblem (TAP) is one kind of classic combinatorial optimization problem whichhas been gained extensive research. Designed an algorithm of TAP based on geneexpression programming (GEP) and implemented it with C# will be presented this paper.At last the analysis and study of experiment is presented, which by a livingexample of people resource assignment. The results indicate this algorithm is correctnessand effectiveness, so provides a reference frame of TAP for some enterpriseunits.
Keyword: task assignment problem; geneexpression programming; inversion
1 引言
任務指派問題(Task Assignment Problem, TAP)是指這樣一類問題：有若干資源和若干任務，如何科學合理的進行資源優化和配置，從而產生最大化的經濟效益和社會效益或者說完成這些任務的成本量最小，即使得指派方案總體效果最佳。這類的問題有廣泛的研究和應用背景，如一個單位有若干項工作需要分配給若干人（或部門）來完成；學校有若干班級需要安排在若干教室裡上課等[1]。
任務指派問題是典型的組合優化問題，是典型的NP問題之一，從而得到了廣泛的關注和研究，有眾多的研究方法解決這類問題，其中有匈牙利法[1]、蟻群算法[2]、模擬退火方法[3]、基於整數規劃的方法[4]等。
基因表達式編程(Gene Expression Programming,GEP) 是由葡萄牙科學家FerreiraC. 2001年提出來的一種新型遺傳算法[5],其特點是將基因型和表現型分離，比傳統的遺傳編程(GeneticProgramming, GP)快2～4個數量級[5]，因而得到了廣泛的關注和研究，已經被廣泛應用到數據挖掘的各個領域[6]。
本文設計了基於GEP思想的TAP問題求解算法，並利用C#編程實現了該算法，同時，通過實例表明算法正確性和有效性。論文余下部分的組織結構如下：第二節闡述了GEP解決TAP問題時染色體結構和遺傳操作；第三節說明了算法設計的整體思路；第四節結合實例，說明算法的運行效率；最後第五節是的結論和下一步工作。
2 基因表達式編程概要
2.1 基因表達式編程算法流程
基因表達式編程(GEP)是將基因型和表現型分開的一種遺傳算法，也就是在該算法中有2個實體：表達樹和染色體，GEP進化中，遺傳操作在固定長度的線性編碼的染色體上進行，而個體評價是在染色體解碼得到的表達樹上進行，即操作和評價相分離。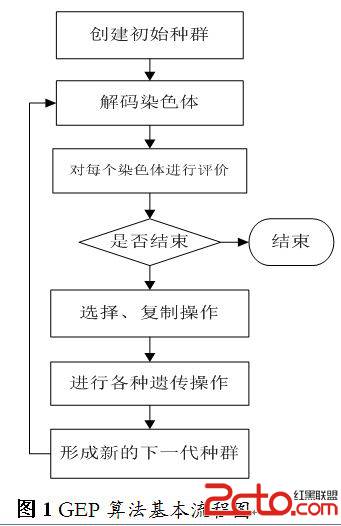
GEP使用Karva語言對表達樹和染色體進行互相編、解碼。染色體由若干個基因組成，每個基因由頭部和尾部組成，頭部可以包含是函數符號和終結符號，尾部僅有終結符號。在GEP中，所有的遺傳操作只要保證基因的合法結構，它就能解碼為合法的程序[10]。
GEP基本算法流程見圖1所示。
正是GEP基因結構性和簡單線性編碼，使得GEP的遺傳算子比較豐富，主要有：變異、逆串、插串、根插串、基因插串、單點重組、2點重組、基因重組等八大算子。其算法的具體技術細節詳解文獻[5]。
2.2 GEP多基因家族結構
對於任務指派問題求解，問題中有兩類信息：資源和任務，每一類信息在GEP的基因表達式中用一個多基因（Multi-gene）結構表示，因此對該問題，使用二基因家族(Multi-geneFamilies)的染色體結構表示。例1是一個簡單例子說明多基因家族問題。
例2 有6個人員和6項任務，每個人完成不同的任務時工作成本不同，我們的問題是，每人安排一項任務，怎樣安排使得完成整個任務的成本最小？
顯然，該問題共有6！種按排方案，是典型的NP問題。我們對人員用數字1-6表示，任務用字母A-F表示。圖2(a)中是GEP解決該問題時一個二基因家族染色體表示，即圖2(b)表示的工作指派方案的信息表示。圖2(b) 表示該染色體解碼對應的表達樹，即圖2(a)染色體的解碼信息，表達了一種任務指派方案。
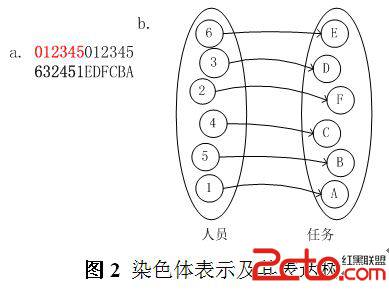需要指出，染色體的編碼是隨機生成，只要保證染色體的合法結構，即串的前6位表示人員信息，後6位表示任務信息，且每種信息是一種排列即可，則每個染色體都能正確的表示一個合法程序，即正確的任務指派方案。
3 主要算法設計
第2節介紹的GEP基本的流程和多基因家族的編碼。本節介紹本算法設計中選擇操作、逆串操作、插串操作和適應度函數的設計問題。
3.1 選擇算子設計
GEP像其它遺傳算法一樣引入隨機選擇方法模擬自然選擇過程，其中輪盤賭方法是一個簡單的實現模擬自然選擇的方式，為了保證進化過程不至於破壞已經獲得的最好解，在輪盤賭的基礎上加了保持最優解的策略。
實現方法是對種群的各個個體進行適應性評價，計算出適應度函數值，然後定義各個個體的選擇概率為個體的適應度函數值與所有適應度函數值的累加和。算法描述如圖3所示。
帶有精英選擇的選擇算法
1
For i=1 to size //size為種群規模
2
計算Fi //Fi是i個體適應度函數值
3
F=sum(Fi) //F適應度函數值之和
4
Fi值最大的個體到下一代第1位置
5
P1=F1/F
6
For i=2 to size //計算累積概率
7
Pi=Pi-1+Fi/F
8
For i=2 to size
9
產生0～1之間隨機數r
10
//根據r值范圍，確定被選中的個體
11
If r<p1 then 選中第一個個體復制
12
Else if r>=pj-1 and r<pj then
13
選擇第j個個體復制到第i位置
圖3 選擇算子算法描述
3.2 遺傳算子設計
本算法主要使用了兩個遺傳操作：逆串（inversion）操作和插串（insertion）操作。逆串操作是指染色體中選擇兩點，把這兩點間的串的順序倒置的操作；插串算子是選擇一個待插入的基因位和一個基因串片斷，將該片斷插入到待插入的基因位，原來位置的基因串依次後退的遺傳操作。例2對這兩種操作做簡單說明。
例2 設父輩染色體如例1所示。即P= 632451EDFCBA。
逆串操作：隨機選擇一個基因家族，如第一個基因家族；再隨機生成0~5之間的兩個隨機數，如2，4，將第2~4位之間基因逆置，得到S=635421 EDFCBA ;
插串操作：隨機選擇一個基因家族，如第一個基因家族；再隨機生成0~5之間隨機數，如2，4，第三步隨機生成0~2（兩個隨機數的最小值）之間隨機數，如1，將第2~4位之間基因插入到1開始的基因位置，其他基因依次後移，得到S=624531EDFCBA 。
逆串遺傳算子的算法描述見圖4所示,插串操作同樣的方法可以設計，這裡因篇幅限制，略去。
逆串遺傳操作算法
1
For i=1 to size //size為種群規模
2
{產生0～1隨機數r
3
If r<pinv then //pinv為逆串率
4
{ p=random(0,1) //隨機選擇0或1
5
If p==0 then//在第一基因家族
6
{產生0~L/2-1之間隨機數r1，r2
7
//L為染色體長度，設r1<r2
8
將r1~r2之間基因取逆放在原位置
9
}else
10
{產生L/2~L之間隨機數r1，r2
11
//設r1<r2
12
將r1~r2之間基因取逆放在原位置
13
}
14
} }
圖4 逆串算子算法描述
3.3 適應度函數設計
適應度函數確定，是進化計算的關鍵問題，它給定了進化計算的進化的方向和速度。TAP問題是一個組合優化問題，目標確定一個最優指派方案。常有2種方法確定這類問題適應度函數。
第一種使用公式(1)確定個體的適應度。
fi＝Tg-Ti＋１ （1）
其中fi為個體i的適應度值，Tg為當前代中成本最大的個體的適應度函數值，Ti為當前代個體i的適應度函數值。這種評價方法簡單實效。
第二種采用公式(2)確定個體適應度。
fi＝Ｍ－Ti； (2)
其中Ｍ為預先指定的一個大數，為固定值。fi，Ti 和第一種評價函數代表的意義相同。這種方法中的Ｍ不太好確定。我們這裡使用公式(1)。
4 實驗分析與研究
4.1 實驗數據及參數
本實驗程序用VS2010環境下C#編寫。
設某單位有6人計劃安排6項任務，每人完成且只完成一項任務，各人的完成每項任務的成本見表1。現在使用本程序求解該問題。
表1 任務指派成本矩陣
A B C D E Ｆ
１
２
３
４
５
６
5 6 9 7 4 6
8 3 5 4 6 7
6 2 4 7 8 9
9 7 6 8 4 5
7 4 3 6 8 9
5 7 8 9 6 4
表2給出實驗參數，進化中選擇函數是具有精英保持策略的輪盤賭算法。
表2 進化中使用參數
參數項
參數值
運行最大代數
200
染色體長度
12
群體規模
10
逆串率
0.25
插串率
0.1
適應度函數
公式(1)
4.2 實驗結果及分析
按表2的進化參數，獨立運行程序100次，平均得到的最小代價約是22。圖4是一次運行的成本變化曲線。
任務指派方案為：426315EDFBAC,即4-E,2-D,6-F,3-B,1-A,5-C。
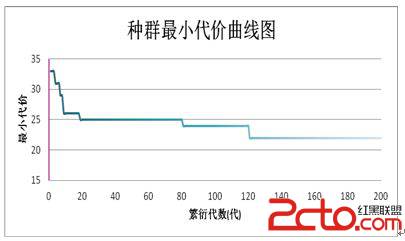圖4 TAP進化過程
該次運行的平均適應度函數值的變化曲線如圖5所示。分析圖4，在前20代系統快速收斂，在100代左右收斂到滿意的近似解，如103代時，最小代價值為23。在120代s時系統趨於穩定。
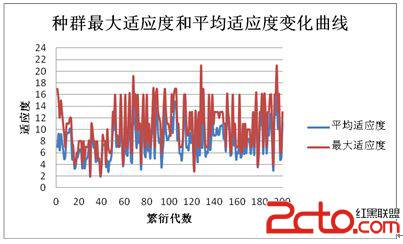圖5 適應度的變化曲線
圖5是運行過程中適應度變化情況，為了清晰，圖中每隔10代取樣一次繪制的圖形。圖5看出，系統進化過程仍保持較高的基因多樣性，所以系統是健康強壯的。
5 結論及下一步工作
GEP是遺傳算法發展的新階段，它繼承了GAs線性定長編碼的優點，又繼承GP對復雜問題的表達能力，從而在基因編碼問題上使用了簡單編碼可以應對復雜的問題[7]。
本文介紹了GEP模型的工作原理，針對TAP問題進行了基於GEP的算法設計，用C#加以實現，進行實驗研究，說明GEP能高效解決TAP問題，下一步工作我們將進一步完善系統，擴大應用，將該工作推廣到實際應用中去。
