在上一篇文章中,已經得到了與正則表達式等價的 NFA,本篇文章會說明如何從 NFA 轉換為 DFA,以及對 DFA 和字符類進行化簡。
一、DFA 的表示
DFA 的表示與 NFA 比較類似,不過要簡單的多,只需要一個添加新狀態的方法即可。Dfa 類的代碼如下所示:
namespace Cyjb.Compilers.Lexers {
class Dfa : IList<DfaState> {
// 在當前 DFA 中創建一個新狀態。
DfaState NewState() {}
}
}
DFA 的狀態也比較簡單,必要的屬性只有兩個:符號索引和狀態轉移。
符號索引表示當前的接受狀態對應的是哪個正則表達式。不過 DFA 的一個狀態可能對應於 NFA 的多個狀態(詳見下面的子集構造法),所以 DFA 狀態的符號索引是一個數組。對於普通狀態,符號索引是空數組。
狀態轉移表示如何從當前狀態轉移到下一狀態,由於在構造 NFA 時已經劃分好了字符類,所以在 DFA 中直接使用數組記錄下不同字符類對應的轉移(DFA 中是不存在 轉移的,而且對每個字符類有且只有一條轉移)。
在 NFA 的狀態定義中,還有一個狀態類型屬性,但是在 DFA 狀態中卻沒有這個屬性,是因為 Trailing 類型的狀態會在 DFA 匹配字符串的時候處理(會在下篇文章中說明),TrailingHead 類型的狀態會在構造 DFA 的時候與 Normal 類型的狀態合並(詳見 2.4 節)。
下面是 DfaState 類的定義:
namespace Cyjb.Compilers.Lexers {
class DfaState {
// 獲取包含當前狀態的 DFA。
Dfa Dfa { get; private set; }
// 獲取或設置當前狀態的索引。
int Index { get; set; }
// 獲取或設置當前狀態的符號索引。
int[] SymbolIndex { get; set; }
// 獲取或設置特定字符類轉移到的狀態。
DfaState this[int charClass] { get; set; }
}
}
DFA 的狀態中額外定義的兩個屬性 Dfa 和 Index 同樣是為了方便狀態的使用。
二、NFA 轉換為 DFA
2.1 子集構造法
將 NFA 轉換為 DFA,采用的是子集構造(subset construction)算法。該算法的過程與《C# 詞法分析器(三)正則表達式》的 3.1 節中提到的 NFA 匹配過程比較相似。在 NFA 的匹配過程中,使用的都是 NFA 的一個狀態集合,那麼子集構造法就是用 DFA 的一個狀態來對應 NFA 的一個狀態集合,即 DFA 讀入輸入字符串 a1a2an 之後到達的狀態,就對應於 NFA 讀入同樣的字符串 a1a2an 之後到達的狀態的集合。
子集構造算法需要用到的操作有:

我們需要找到的是當一個 NFA N 讀入了某個輸入串後,可能位於的所有狀態集合。
首先,在讀入第一個字符之前,N 可以位於 -closure(s0) 中的任何狀態,其中 s0 是 N 的開始狀態。那麼,此時 -closure(s0) 就表示 DFA 的開始狀態。
假設 N 在讀入輸入串 x 之後可以位於集合 T 中的狀態上,下一個輸入字符是 a,那麼 N 可以立即移動到 move(T,a) 中的任何狀態,並且還可以通過 轉移來移動到 -closure(move(T,a)) 中的任何狀態上。這樣的每個不同的 -closure(move(T,a)) 就表示了一個 DFA 的狀態。如果這個說明難以理解,可以參考後面給出的示例。
據此,可以得到以下的算法(算法中的 T[a]=U 表示在狀態 T 中的字符類 a 上存在到狀態 U 的轉移):
輸入:一個 NFA N
輸出:與 NFA 等價的 DFA D
一開始,-closure(s0) 是 D 中的唯一狀態,且未被標記
while (在 D 中存在未被標記的狀態 T) {
為 T 加上標記
foreach (每個字符類 a) {
U=-closure(move(T,a))
if (U 不在 D 中) {
將 U 加入 D 中,且未被標記
}
T[a]=U
}
}
如果某個 NFA 是終結狀態,那麼所有包含它的 DFA 狀態也是終結狀態,而且 DFA 狀態的符號索引就包含 NFA 狀態對應的符號索引。一個 DFA 狀態可能對應於多個 NFA 狀態,所以上面定義 DfaState 時,符號索引是一個數組。
計算 -closure(T) 的過程就是從一個狀態集合開始的簡單圖搜索過程,使用 DFS 即可實現,具體的算法如下(-closure(s) 的算法也同理,等價於 -closure({s})):
輸入:NFA 的狀態集合 T
輸出:-closure(T)
將 T 的所有狀態壓入堆棧
-closure(T)=T
while (堆棧非空) {
彈出棧頂元素 t
foreach (u : t 可以通過 轉移到達 u) {
if (u-closure(T)) {
-closure(T)=-closure(T)∪{u}
將 u 壓入堆棧
}
}
}
計算 move(T,a) 的算法更加簡單,只有一個循環:
輸入:NFA 的狀態集合 T
輸出:move(T,a)
move(T,a)=
foreach (u∈T) {
if (u 存在字符類 a 上的轉移,目標為 t) {
move(T,a)=move(T,a)∪{t}
}
}
2.2 子集構造法的示例
這裡以上一節中從正則表達式 (a|b)*baa 構造得到的 NFA 作為示例,將它轉化為 DFA。這裡的輸入字母表 Σ={a,b}。
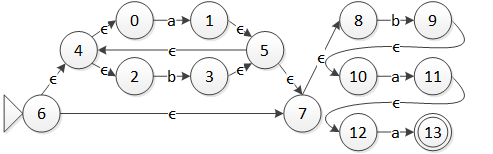
圖 1 正則表達式 (a|b)*baa 的 NFA

圖 2 構造 DFA 的示例

圖 3 最終得到的 DFA
2.3 多個首狀態的子集構造法
上一節中構造得到的 NFA 是具有多個開始狀態的(為了支持上下文和行首限定符),不過對子集構造法並不會產生影響,因為子集構造法是從開始狀態開始,沿著 NFA 的轉移不斷構造相應的 DFA 狀態,只要對多個開始狀態分別調用自己構造法就可以正確構造出多個 DFA,而且不必擔心 DFA 之間的相互影響。為了方便起見,這多個 DFA 仍然保存在一個 DFA 中,只不過還是使用起始狀態來進行區分。
2.4 DFA 狀態的符號索引
一個 DFA 狀態對應 NFA 的一個狀態集合,那麼直接將這多個 NFA 狀態的符號索引全都拿來就可以了。不過前面說到, TrailingHead 類型的 NFA 狀態會在構造 DFA 的時候與 Normal 類型的 NFA 狀態合並,這個合並指的就是符號索引的合並。
這個合並的方法也很簡單,Normal 類型的狀態直接將符號索引拿來,TrailingHead 類型的狀態,則將 int.MaxValue - SymbolIndex 的值作為 DFA 狀態的符號索引,這樣兩種類型的狀態就可以區分出來(由於定義的符號數不會太多,所以不必擔心出現重復或者負值)。
最後,再對 DFA 狀態的符號索引從小到大進行排序。這樣就會使 Normal 類型狀態的符號索引總是排在 TrailingHead 類型狀態的符號索引的前面,在後面進行詞法分析時能夠更容易處理,效率也會有略微的提升。
2.5 子集構造法的實現
子集構造法的 C# 實現與上面給出的偽代碼基本一致,不過這裡有個問題需要解決,就是如何高效的從 NFA 的狀態集合得到相應的 DFA 狀態。由於 NFA 狀態集合是采用 HashSet<NfaState> 來保存的,所以我直接利用 Dictionary<HashSet<NfaState>, DfaState> 來解決這個問題,這裡需要采用自定義的弱哈希函數,使得集合對應的哈希值只與集合中的元素相關,而與元素順序無關。
下面就是定義在 Nfa 類中的方法:
/// <summary>
/// 根據當前的 NFA 構造 DFA,采用子集構造法。
/// </summary>
/// <param name="headCnt">頭節點的個數。</param>
internal Dfa BuildDfa(int headCnt) {
Dfa dfa = new Dfa(charClass);
// DFA 和 NFA 的狀態映射表,DFA 的一個狀態對應 NFA 的一個狀態集合。
Dictionary<DfaState, HashSet<NfaState>> stateMap =
new Dictionary<DfaState, HashSet<NfaState>>();
// 由 NFA 狀態集合到對應的 DFA 狀態的映射表(與上表互逆)。
Dictionary<HashSet<NfaState>, DfaState> dfaStateMap =
new Dictionary<HashSet<NfaState>, DfaState>(SetEqualityComparer<NfaState>.Default);
Stack<DfaState> stack = new Stack<DfaState>();
// 添加頭節點。
for (int i = 0; i < headCnt; i++) {
DfaState head = dfa.NewState();
head.SymbolIndex = new int[0];
HashSet<NfaState> headStates = EpsilonClosure(Enumerable.Repeat(this[i], 1));
stateMap.Add(head, headStates);
dfaStateMap.Add(headStates, head);
stack.Push(head);
}
int charClassCnt = charClass.Count;
while (stack.Count > 0) {
DfaState state = stack.Pop();
HashSet<NfaState> stateSet = stateMap[state];
// 遍歷字符類。
for (int i = 0; i < charClassCnt; i++) {
// 對於 NFA 中的每個轉移,尋找 Move 集合。
HashSet<NfaState> set = Move(stateSet, i);
if (set.Count > 0) {
set = EpsilonClosure(set);
DfaState newState;
if (!dfaStateMap.TryGetValue(set, out newState)) {
// 添加新狀態.
newState = dfa.NewState();
stateMap.Add(newState, set);
dfaStateMap.Add(set, newState);
stack.Push(newState);
// 合並符號索引。
newState.SymbolIndex = set.Where(s => s.SymbolIndex != Symbol.None)
.Select(s => {
if (s.StateType == NfaStateType.TrailingHead) {
return int.MaxValue - s.SymbolIndex;
} else {
return s.SymbolIndex;
}
}).OrderBy(idx => idx).ToArray();
}
// 添加 DFA 的轉移。
state[i] = newState;
}
}
}
return dfa;
}
/// <summary>
/// 返回指定 NFA 狀態集合的 閉包。
/// </summary>
/// <param name="states">要獲取 閉包的 NFA 狀態集合。</param>
/// <returns>得到的 閉包。</returns>
private static HashSet<NfaState> EpsilonClosure(IEnumerable<NfaState> states) {
HashSet<NfaState> set = new HashSet<NfaState>();
Stack<NfaState> stack = new Stack<NfaState>(states);
while (stack.Count > 0) {
NfaState state = stack.Pop();
set.Add(state);
// 這裡只需遍歷 轉移。
int cnt = state.EpsilonTransitions.Count;
for (int i = 0; i < cnt; i++) {
NfaState target = state.EpsilonTransitions[i];
if (set.Add(target)) {
stack.Push(target);
}
}
}
return set;
}
/// <summary>
/// 返回指定 NFA 狀態集合的字符類轉移集合。
/// </summary>
/// <param name="states">要獲取字符類轉移集合的 NFA 狀態集合。</param>
/// <param name="charClass">轉移使用的字符類。</param>
/// <returns>得到的字符類轉移集合。</returns>
private static HashSet<NfaState> Move(IEnumerable<NfaState> states, int charClass) {
HashSet<NfaState> set = new HashSet<NfaState>();
foreach (NfaState state in states) {
if (state.CharClassTransition != null && state.CharClassTransition.Contains(charClass)) {
set.Add(state.CharClassTarget);
}
}
return set;
}
在這個實現中,將 DFA 的起始狀態的符號索引設為了空數組,這樣會使得空字符串 不會被匹配(其它匹配不會受到影響),即 DFA 至少會匹配一個字符。這樣的做法在詞法分析中是有意義的,因為詞素不能是空字符串。
2.6 DFA 中的死狀態
嚴格說來,由以上的算法得到的 DFA 可能並不是一個 DFA,因為 DFA 要求每個狀態在每個字符類上有且只有一個轉移。而上面的算法生成的 DFA,在某些字符類上可能並沒有的轉移,因為在算法中,如果這個轉移對應的 NFA 狀態集合是空集,則無視這個轉移。如果是嚴格的 DFA 的話,這時應該添加一個到死狀態 的轉移(死狀態在所有字符類上的轉移都到達其自身)。
但是在詞法分析中,需要知道什麼時候已經不存在被這個 DFA 接受的可能性了,這樣才能夠知道是否已經匹配到了正確的詞素。因此,在詞法分析中,到達死狀態的轉移將被消除,如果沒有找到某個輸入符號上的轉換,就認為這時候已經匹配到了正確的詞素(最後一個終結狀態對應的詞素)。
三、DFA 的化簡
3.1 DFA 最小化
上面雖然構造出了一個可用的 DFA,但它可能並不是最優的,例如下面的兩個等價的 DFA,識別的都是正則表達式 (a|b)*baa,但具有不同的狀態數。
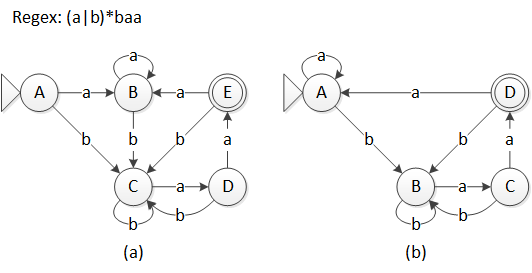
圖 4 兩個等價的 DFA
查看本欄目
3.2 DFA 最小化的示例
下面以圖 4(a) 為例,給出 DFA 最小化的示例。
初始的劃分包括兩個組 {A,B,C,D} 和 {E},分別是非接受狀態組和接受狀態組。
第一次分割,在 {A,B,C,D} 組中,對於字符 a,狀態 A,B,C 都轉移到組內的狀態,而狀態 D 轉移到組 {E} 中,所以狀態 D 需要被劃分出來。對於字符 b,所有狀態都轉移到該組內的狀態,不能區分;{E} 組中,只含有一個狀態,無需進一步劃分。這一輪 Πnew={{A,B,C},{D},{E}}。
第二次分割,在 {A,B,C} 組中,對於字符 a,狀態 A,B 都轉移到組內的狀態,而狀態 C 轉移到組 {D} 中,對於字符 b 則不能區分;組 {D} 和組 {E} 同樣不做劃分。這一輪 Πnew={{A,B},{C},{D},{E}}。
第三次分割,唯一可能被分割的組 {A,B},對於字符 a 和字符 b,都會轉移到相同的組內,所以不會被分割。因此就得到 Πfinal={{A,B},{C},{D},{E}}。
最後,構造出最小化的 DFA,它有四個狀態,對應於 Πfinal 的四個分組。分別挑選 A,C,D,E 作為每個分組的代表,其中,A 是開始狀態,E 是接受狀態。將所有狀態到 B 的轉移都修改為到 A 的轉移,最後得到的 DFA 轉換表為:
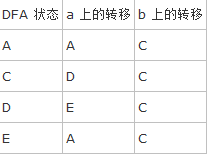
最後再將狀態重新排序,得到的就是如圖 4(b) 所示的 DFA 了。
3.3 字符類最小化
在 DFA 最小化之後,還要將字符類也最小化,因為 DFA 的最小化過程會合並等價狀態,這時可能會使得某些字符類變得等價,如圖 5 所示。
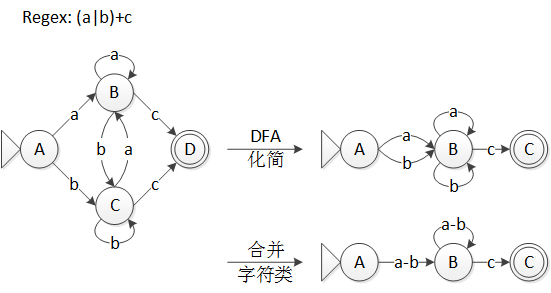
圖 5 等價的字符類
等價字符類的尋找比等價狀態更簡單些,先將化簡後的 DFA 用表格的形式寫出來,以圖 5 中的 DFA 為例:
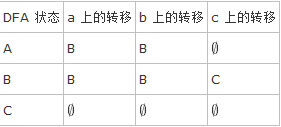
表格中的第一列是 DFA 的狀態,後面的三列分別代表不同字符類上的轉移。表格的第二行到第四行分別對應著 A、B、C 三個狀態的轉移。那麼,如果在這個表格中某兩列完全相同,那麼對應的字符類就是等價的。
化簡 DFA 和字符類的實現代碼比較多,這裡就不貼了,請參見 Dfa 類。
最後化簡得到的 DFA,一般是用轉移表的形式保存(即上面的表格形式),使用下面三個數組就可以完整表示出 DFA 了。
int[] CharClass; int[,] Transitions; int[][] SymbolIndex;
其中,CharClass 是字符類的映射表,它是長為 65536 的數組,用於將字符映射為相應的字符類;Transitions 是 DFA 的轉移表,行數等於 DFA 中的狀態數,列數為字符類的個數;SymbolIndex 則是每個狀態對應的符號索引。而在實際的代碼中,為了兼顧可用性,表示與此略有不同。
當然也可以對 DFA 的轉移表和符號索引進行壓縮以節約內存,不過這個留在以後再說。
下一篇就會介紹如何以 DFA 為基礎,構造一個詞法分析器。
作者:CYJB
出處:http://www.cnblogs.com/cyjb/