簡介
樹是一種非線性結構。樹的本質是將一些節點由邊連接起來,形成層級的結構。而二叉樹是一種特殊的樹,使得樹每個子節點必須小於等於2.而二叉查找樹又是一類特殊的二叉樹。使得每一個節點的左節點或左子樹的所有節點必須小於這個節點,右節點必須大於這個節點。從而方便高效搜索。
下面來看如何使用C#實現二叉查找樹。
實現節點
二叉查找樹是節點的集合。因此首先要構建節點,如代碼1所示。
//二叉查找樹的節點定義publicclass Node
{
//節點本身的數據publicint data;
//左孩子public Node left;
//右孩子public Node right;
publicvoid DisplayData()
{
Console.Write(data+"");
}
}
代碼1.節點的定義
構建二叉樹
構建二叉樹是通過向二叉樹插入元素得以實現的,所有小於根節點的節點插入根節點的左子樹,大於根節點的,插入右子樹。依此類推進行遞歸。直到找到位置進行插入。二叉查找樹的構建過程其實就是節點的插入過程。C#實現代碼如代碼2所示。
publicvoid Insert(int data)
{
Node Parent;
//將所需插入的數據包裝進節點
Node newNode=new Node();
newNode.data=data;
//如果為空樹,則插入根節點if(rootNode==null)
{
rootNode=newNode;
}
//否則找到合適葉子節點位置插入else
{
Node Current = rootNode;
while(true)
{
Parent=Current;
if(newNode.data<Current.data)
{
Current=Current.left;
if(Current==null)
{
Parent.left=newNode;
//插入葉子後跳出循環break;
}
}
else
{
Current = Current.right;
if (Current == null)
{
Parent.right = newNode;
//插入葉子後跳出循環break;
}
}
}
}
}
代碼2.實現二叉樹的插入
二叉樹的遍歷
二叉樹的遍歷分為先序(PreOrder),中序(InOrder)和後序(PostOrder)。先序首先遍歷根節點,然後是左子樹,然後是右子樹。中序首先遍歷左子樹,然後是根節點,最後是右子樹。而後續首先遍歷左子樹,然後是右子樹,最後是根節點。因此,我們可以通過C#遞歸來實現這三種遍歷,如代碼3所示。
//中序publicvoid InOrder(Node theRoot)
{
if (theRoot != null)
{
InOrder(theRoot.left);
theRoot.DisplayData();
InOrder(theRoot.right);
}
}
//先序publicvoid PreOrder(Node theRoot)
{
if (theRoot != null)
{
theRoot.DisplayData();
PreOrder(theRoot.left);
PreOrder(theRoot.right);
}
}
//後序publicvoid PostOrder(Node theRoot)
{
if (theRoot != null)
{
PostOrder(theRoot.left);
PostOrder(theRoot.right);
theRoot.DisplayData();
}
}
代碼3.實現二叉排序樹的先序,中序和後續遍歷
找到二叉查找樹中的最大值和最小值
二叉查找樹因為已經有序,所以查找最大值和最小值非常簡單,找最小值只需要找最左邊的葉子節點即可。而找最大值也僅需要找最右邊的葉子節點,如代碼4所示。
//找到最大節點publicvoid FindMax()
{
Node current = rootNode;
//找到最右邊的節點即可while (current.right != null)
{
current = current.right;
}
Console.WriteLine("n最大節點為:" + current.data);
}
//找到最小節點publicvoid FindMin()
{
Node current = rootNode;
//找到最左邊的節點即可while (current.left != null)
{
current = current.left;
}
Console.WriteLine("n最小節點為:" + current.data);
}
代碼4.二叉查找樹找最小和最大節點
二叉查找樹的查找
因為二叉查找樹已經有序,所以查找時只需要從根節點開始比較,如果小於根節點,則查左子樹,如果大於根節點,則查右子樹。如此遞歸,如代碼5所示。
//查找public Node Search(int i)
{
Node current = rootNode;
while (true)
{
if (i < current.data)
{
if (current.left == null)
break;
current = current.left;
}
elseif (i > current.data)
{
if (current == null)
break;
current = current.right;
}
else
{
return current;
}
}
if (current.data != i)
{
returnnull;
}
return current;
}
代碼5.二叉查找樹的查找
二叉樹的刪除
二叉樹的刪除是最麻煩的,需要考慮四種情況:
被刪節點是葉子節點
被刪節點有左孩子沒右孩子
被刪節點有右孩子沒左孩子
被刪節點有兩個孩子
我們首先需要找到被刪除的節點和其父節點,然後根據上述四種情況分別處理。如果遇到被刪除元素是根節點時,還需要特殊處理。如代碼6所示。
//刪除二叉查找樹中的節點,最麻煩的操作public Node Delete(int key)
{
Node parent = rootNode;
Node current = rootNode;
//首先找到需要被刪除的節點&其父節點while (true)
{
if (key < current.data)
{
if (current.left == null)
break;
parent = current;
current = current.left;
}
elseif (key > current.data)
{
if (current == null)
break;
parent = current;
current = current.right;
}
//找到被刪除節點,跳出循環else
{
break;
}
}
//找到被刪除節點後,分四種情況進行處理//情況一,所刪節點是葉子節點時,直接刪除即可if (current.left == null && current.right == null)
{
//如果被刪節點是根節點,且沒有左右孩子if (current == rootNode&&rootNode.left==null&&rootNode.right==null)
{
rootNode = null;
}
elseif (current.data < parent.data)
parent.left = null;
else
parent.right = null;
}
//情況二,所刪節點只有左孩子節點時elseif(current.left!=null&¤t.right==null)
{
if (current.data < parent.data)
parent.left = current.left;
else
parent.right = current.left;
}
//情況三,所刪節點只有右孩子節點時elseif (current.left == null && current.right != null)
{
if (current.data < parent.data)
parent.left = current.right;
else
parent.right = current.right;
}
//情況四,所刪節點有左右兩個孩子else
{
//current是被刪的節點,temp是被刪左子樹最右邊的節點
Node temp;
//先判斷是父節點的左孩子還是右孩子if (current.data < parent.data)
{
parent.left = current.left;
temp = current.left;
//尋找被刪除節點最深的右孩子while (temp.right != null)
{
temp = temp.right;
}
temp.right = current.right;
}
//右孩子elseif (current.data > parent.data)
{
parent.right = current.left;
temp = current.left;
//尋找被刪除節點最深的左孩子while (temp.left != null)
{
temp = temp.left;
}
temp.right = current.right;
}
//當被刪節點是根節點,並且有兩個孩子時else
{
temp = current.left;
while (temp.right != null)
{
temp = temp.right;
}
temp.right = rootNode.right;
rootNode = current.left;
}
}
return current;
}
代碼6.二叉查找樹的刪除
測試二叉查找樹
現在我們已經完成了二叉查找樹所需的各個功能,下面我們來對代碼進行測試:
BinarySearchTree b = new BinarySearchTree();
/*插入節點*/
b.Insert(5);
b.Insert(7);
b.Insert(1);
b.Insert(12);
b.Insert(32);
b.Insert(15);
b.Insert(22);
b.Insert(2);
b.Insert(6);
b.Insert(24);
b.Insert(17);
b.Insert(14);
/*插入結束 *//*對二叉查找樹分別進行中序,先序,後序遍歷*/
Console.Write("n中序遍歷為:");
b.InOrder(b.rootNode);
Console.Write("n先序遍歷為:");
b.PreOrder(b.rootNode);
Console.Write("n後序遍歷為:");
b.PostOrder(b.rootNode);
Console.WriteLine("");
/*遍歷結束*//*查最大值和最小值*/
b.FindMax();
b.FindMin();
/*查找結束*//*搜索節點*/
Node x = b.Search(15);
Console.WriteLine("n所查找的節點為" + x.data);
/*搜索結束*//*測試刪除*/
b.Delete(24);
Console.Write("n刪除節點後先序遍歷的結果是:");
b.InOrder(b.rootNode);
b.Delete(5);
Console.Write("n刪除根節點後先序遍歷的結果是:");
b.InOrder(b.rootNode);
Console.ReadKey();
/*刪除結束*/
代碼7.測試二叉查找樹
運行結果如圖1所示:
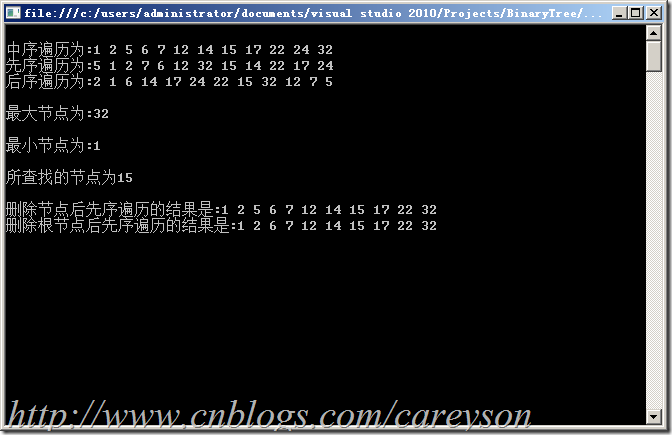
圖1.測試運行結果
總結
樹是節點的層級集合,而二叉樹又是將每個節點的孩子限制為小於等於2的特殊樹,二叉查找樹又是一種特殊的二叉樹。二叉樹對於查找來說是非常高效,尤其是查找最大值和最小值。