1.等本息法月還款額計算公式的推導
在上一篇隨筆“用 C# 寫個人住房貸款計算器”中提到,等本息法在利率不變的情況下,每月的還款額是固定的,所以也稱為“等額法”,計算公式如下:
月還款額 = 貸款金額 x 月利率 x (1 + 月利率)期數
現在就讓我們來推導出這個公式吧。
我們知道,等本息法的計算方法如下:
本月月還利息 = 上月剩余貸款余額 x 月利率
本月月還本金 = 月還款額 - 本月月還利息
本月剩余貸款余額 = 上月剩余貸款余額 - 本月月還本金
因此:
本月剩余貸款余額
= 上月剩余貸款余額 - 本月月還本金
= 上月剩余貸款余額 - (月還款額 - 本月月還利息)
= 上月剩余貸款余額 - 月還款額 + 本月月還利息
= 上月剩余貸款余額 - 月還款額 + 上月剩余貸款額 x 月利率
= 上月剩余貸款余額 x (1 + 月利率) - 月還款額
設:
A = 貸款金額
r = 月利率
n = 期數
z = 月還款額
這樣,各個月的剩余貸款余額如下表:
根據上表,最後一期的剩余貸款余額是:
A(1+r)n – z[(1+r)n-1 + … + (1+r) + 1] = A(1+r)n – z[(1+r)n - 1] / r
上面的計算是根據等比數列的求和公式,Sn = a1(qn – 1) / (q – 1),其中 a1 = 1,q = 1+r 。
由於最後一期的剩余貸款余額必須為零,因此:
A(1+r)n – z[(1+r)n - 1] / r = 0
z[(1+r)n - 1] / r = A(1+r)n
z = A · r · (1+r)n / [(1+r)n - 1]
這就是本文一開頭提到的等本息法月還款額的計算公式。
2.等本息法應付的總利息
在利率不變的情況下,等本息法的月還款額是固定的,計算公式如下:
月還款額 = 貸款金額 x 月利率 x (1+月利率)期數 / [(1+月利率)期數 - 1]
本月月還利息 = 上月剩余貸款余額 x 月利率
本月月還本金 = 月還款額 - 本月月還利息
本月剩余貸款余額 = 上月剩余貸款余額 - 本月月還本金
因此:
總利息 = 總還款額 - 貸款金額 = 月還款額 x 期數 - 貸款金額 = z · n - A
將月還款額 z = A · r · (1+r)n / [(1+r)n - 1] 代入上式,得到:
總利息 = A · [1 + (n · r - 1) · (1+r)n] / [(1+r)n - 1]
上式中,貸款金額 A 和月利率 r 都是正實數,期數 n 是正整數。
思考題:
證明:按上式計算的總利息大於零。
當月利率 r 趨向於零時,按上式計算的總利息的極限是多少?
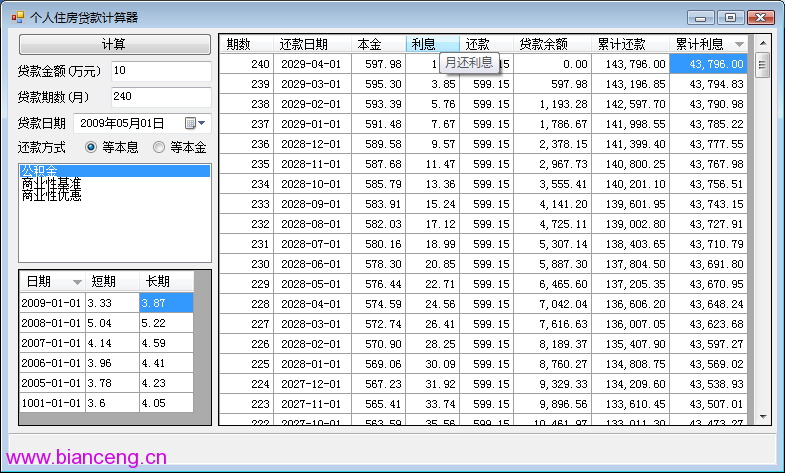
當貸款金額 A = 10 萬元,月利率 r = 3.87% / 12,期數 n = 240 時,代入上式計算得到的總利息是 43,796.52 元。下圖中使用個人住房貸款計算器計算出來的總利息是 43,796.00 元,兩者相差 0.52 元,是因為該計算器在計算還款計劃表時各個月的月還利息都必須進行捨入處理造成的。
3.等本金法應付的總利息
在利率不變的情況下,等本金法的月還本金是固定的,計算公式如下:
月還本金 = 貸款金額 / 期數
本月月還利息 = 上月剩余貸款余額 x 月利率
本月月還款額 = 月還本金 + 本月月還利息
本月剩余貸款余額 = 上月剩余貸款余額 - 月還本金
這樣,各個月的月還利息如下表:
因此,將上表中各個月的月還利息加起來就得到:
總利息 = r · A · n – r · A · n · [0 + (n-1)/n] / 2
上面的計算是根據等差數列的求和公式,Sn = n · (a1 + an) / 2,其中 a1 = 0,an = (n-1)/n 。
化簡後得到:
總利息 = A · r · (n+1) / 2
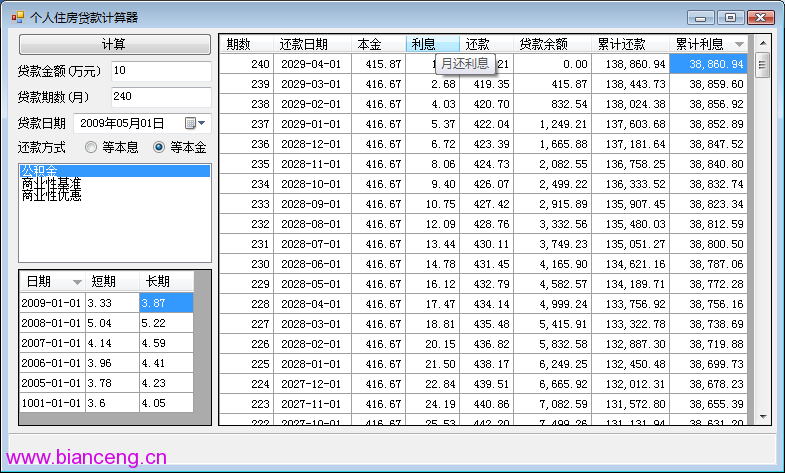
當貸款金額 A = 10 萬元,月利率 r = 3.87% / 12,期數 n = 240 時,代入上式計算得到的總利息是 38,861.25 元。下圖中使用個人住房貸款計算器計算出來的總利息是 38,860.94 元,兩者相差 0.31 元,是因為該計算器在計算還款計劃表時各個月的月還利息都必須進行捨入處理造成的。
4.等本息法和等本金法應付的總利息的比較
那麼,在貸款金額、利率和期限相同的情況下,哪種還款方式的成本更小呢?
在上面兩個小節中,我們看到,當貸款金額為 10 萬元,年利率為 3.87%,期限為 20 年時,等本息法應付的總利息為 43,796.00 元,而等本金法為 38,860.94 元,兩者相差 4,935.06 元。
但是,在上述情況下,等本息法的月還款額固定為 599.15 元。而等本金法的月還款額第一個月為 739.17 元,以後逐月遞減,直到最後一個月為 417.21 元。
可見,如果經濟能力能夠負擔剛開始時比較大的月還款額,應該選擇等本金法,可以節省不少利息。
當然,上面僅僅是一個特定的例子,並不是證明在所有情況下等本金法都會比等本息法節省利息。
根據前面的兩個小節,我們知道:
等本息法的總利息 = A · [1 + (n · r - 1) · (1+r)n] / [(1+r)n - 1]
等本金法的總利息 = A · r · (n+1) / 2
利息差 = A · { [1 + (n · r - 1) · (1+r)n] / [(1+r)n - 1] - r · (n+1) / 2 }
上面的算式中,貸款金額 A 和月利率 r 都是正實數,期數 n 是正整數。
目前我還沒有找到證明利息差不小於零的方法。
下面是利息差關於月利率 r 的函數的圖像,坐標原點在左下角,貸款金額為1元,期數為180個月,年利率從0%變化到10%,函數值(利息差)從0元變化到0.18元。
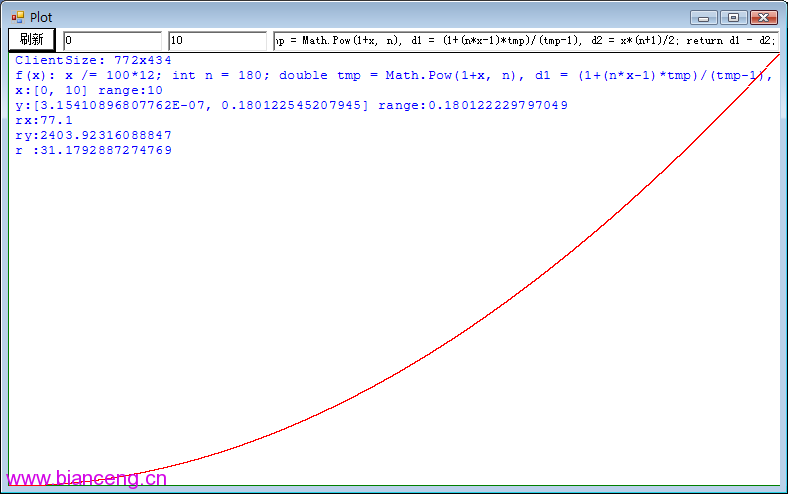
上面的 Plot 程序請參見我在2005年11月1日發表的隨筆“畫函數圖形的C#程序(改進版)”。
5.利率為零時的情況
如果天上掉餡餅下來,貸款的利率為零的話,月還利息就為零,月還款額等於月還本金,等於貸款金額除以期數,對於等本息法就和等本金法都是這樣的。
在前面的第1小節,我們證明了等本息法的月還款額由以下公式決定:
z = A · r · (1+r)n / [(1+r)n - 1]
上式在月利率 r 趨向於零時的極限:
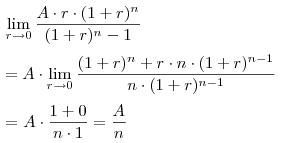
上面的計算中用到的規則:
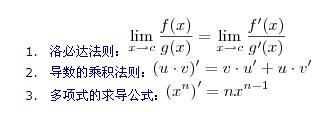
其實,這個極限這也可以用初等方法(即不使用微積分)解出,如下:

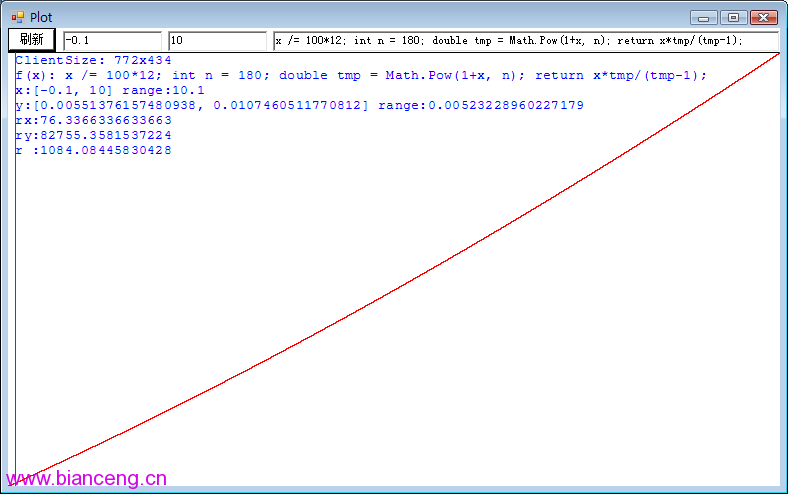
下面是等本息法的月還款額關於月利率 r 的函數的圖像,貸款金額為1元,期數為180個月,年利率從 -0.1% 變化到 10% ,函數值(月還款額)從 0.005514 元變化為 0.010746 元。注意:A/n = 1/180 = 0.005555… 。