1. 簡介
紅黑樹是一種自平衡二叉查找樹。它的統計性能要好於平衡二叉樹(AVL樹),因此,紅黑樹在很多地方都有應用。在C++ STL中,很多部分(目前包括set, multiset, map, multimap)應用了紅黑樹的變體(SGI STL中的紅黑樹有一些變化,這些修改提供了更好的性能,以及對set操作的支持)。它是復雜的,但它的操作有著良好的最壞情況運行時間,並且在實踐中是高效的: 它可以在O(log n)時間內做查找,插入和刪除等操作。
本文介紹了紅黑樹的基本性質和基本操作。
2. 紅黑樹的性質
紅黑樹,顧名思義,通過紅黑兩種顏色域保證樹的高度近似平衡。它的每個節點是一個五元組:color(顏色),key(數據),left(左孩子),right(右孩子)和p(父節點)。
紅黑樹的定義也是它的性質,有以下五條:
性質1. 節點是紅色或黑色
性質2. 根是黑色
性質3. 所有葉子都是黑色(葉子是NIL節點)
性質4. 如果一個節點是紅的,則它的兩個兒子都是黑的
性質5. 從任一節點到其葉子的所有簡單路徑都包含相同數目的黑色節點。
這五個性質強制了紅黑樹的關鍵性質: 從根到葉子的最長的可能路徑不多於最短的可能路徑的兩倍長。為什麼呢?性質4暗示著任何一個簡單路徑上不能有兩個毗連的紅色節點,這樣,最短的可能路徑全是黑色節點,最長的可能路徑有交替的紅色和黑色節點。同時根據性質5知道:所有最長的路徑都有相同數目的黑色節點,這就表明了沒有路徑能多於任何其他路徑的兩倍長。
3. 紅黑樹的基本操作
因為紅黑樹也是二叉查找樹,因此紅黑樹上的查找操作與普通二叉查找樹上的查找操作相同。然而,紅黑樹上的插入操作和刪除操作會導致不再符合紅黑樹的性質。恢復紅黑樹的性質需要少量(O(log n))的顏色變更(實際是非常快速的)和不超過三次樹旋轉(對於插入操作是兩次)。雖然插入和刪除很復雜,但操作時間仍可以保持為 O(log n) 次。
3.1 插入操作
插入操作可以概括為以下幾個步驟:
(1) 查找要插入的位置,時間復雜度為:O(N)
(2) 將新節點的color賦為紅色
(3) 自下而上重新調整該樹為紅黑樹
其中,第(1)步的查找方法跟普通二叉查找樹一樣,第(2)步之所以將新插入的節點的顏色賦為紅色,是因為:如果設為黑色,就會導致根到葉子的路徑上有一條路上,多一個額外的黑節點,這個是很難調整的。但是設為紅色節點後,可能會導致出現兩個連續紅色節點的沖突,那麼可以通過顏色調換(color flips)和樹旋轉來調整,這樣簡單多了。下面討論步驟(3)的一些細節:
設要插入的節點為N,其父節點為P,其父親G的兄弟節點為U(即P和U是同一個節點的兩個子節點)。
[1] 如果P是黑色的,則整棵樹不必調整便是紅黑樹。
[2] 如果P是紅色的(可知,其父節點G一定是黑色的),則插入z後,違背了性質4,需要進行調整。調整時分以下3種情況:
(a)N的叔叔U是紅色的
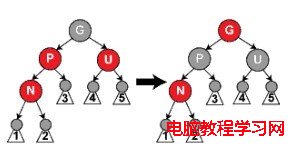
如上圖所示,我們將P和U重繪為黑色並重繪節點G為紅色(用來保持性質5)。現在新節點N有了一個黑色的父節點P,因為通過父節點P或叔父節點U的任何路徑都必定通過祖父節點G,在這些路徑上的黑節點數目沒有改變。但是,紅色的祖父節點G的父節點也有可能是紅色的,這就違反了性質4。為了解決這個問題,我們在祖父節點G上遞歸調整顏色。
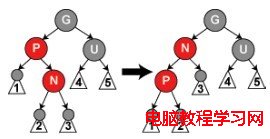
(b)N的叔叔U是黑色的,且N是右孩子

如上圖所示,我們對P進行一次左旋轉調換新節點和其父節點的角色; 接著,按情形(c)處理以前的父節點P以解決仍然失效的性質4。
(c)N的叔叔U是黑色的,且N是左孩子
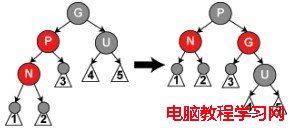
如上圖所示,對祖父節點G 的一次右旋轉; 在旋轉產生的樹中,以前的父節點P現在是新節點N和以前的祖父節點G 的父節點, 然後交換以前的父節點P和祖父節點G的顏色,結果的樹滿足性質4,同時性質5[4]也仍然保持滿足。
3.2 刪除操作
刪除操作可以概括為以下幾個步驟:
(1) 查找要刪除位置,時間復雜度為:O(N)
(2) 用刪除節點後繼或者節點替換該節點(只進行數據替換即可,不必調整指針,後繼節點是中序遍歷中緊挨著該節點的節點,即:右孩子的最左孩子節點)
(3) 如果刪除節點的替換節點為黑色,則需重新調整該樹為紅黑樹
其中,第(1)步的查找方法跟普通二叉查找樹一樣,第(2)步之所以用後繼節點替換刪除節點,是因為這樣可以保證該後繼節點之上仍是一個紅黑樹,而後繼節點可能是一個葉節點或者只有右子樹的節點,這樣只需用有節點替換後繼節點即可達到刪除的目的。如果需要刪除的節點有兩個兒子,那麼問題可以被轉化成刪除另一個只有一個兒子的節點的問題。(沒看懂???可參考:http://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91 )在第(3)步中,如果,如果刪除節點為紅色節點,則他的父親和孩子全為黑節點,這樣直接刪除該節點即可,不必進行任何調整。如果刪除節點是黑節點,分四種情況:
設要刪除的節點為N,其父節點為P,其兄弟節點為S。
由於N是黑色的,則P可能是黑色的,也可能是紅色的,S也可能是黑色的或者紅色的
(1)S是紅色的
此時P肯定是紅色的。我們對N的父節點進行左旋轉,然後把紅色兄弟轉換成N的祖父。我們接著對調 N 的父親和祖父的顏色。盡管所有的路徑仍然有相同數目的黑色節點,現在 N 有了一個黑色的兄弟和一個紅色的父親,所以我們可以接下去按 (2)、(3)或(4)情況來處理。
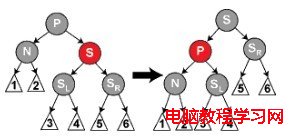
(2)S和S的孩子全是黑色的
在這種情況下,P可能是黑色的或者紅色的,我們簡單的重繪S 為紅色。結果是通過S的所有路徑,它們就是以前不通過 N 的那些路徑,都少了一個黑色節點。因為刪除 N 的初始的父親使通過 N 的所有路徑少了一個黑色節點,這使事情都平衡了起來。但是,通過 P 的所有路徑現在比不通過 P 的路徑少了一個黑色節點。接下來,要調整以P作為N遞歸調整樹。
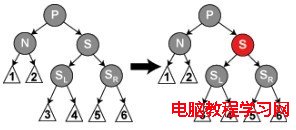
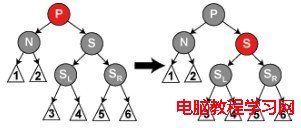
(3)S是黑色的,S的左孩子是紅色,右孩子是黑色
這種情況下我們在 S 上做右旋轉,這樣 S 的左兒子成為 S 的父親和 N 的新兄弟。我們接著交換 S 和它的新父親的顏色。所有路徑仍有同樣數目的黑色節點,但是現在 N 有了一個右兒子是紅色的黑色兄弟,所以我們進入了情況(4)。N 和它的父親都不受這個變換的影響。
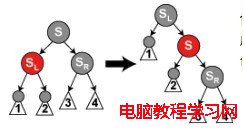
(4)S是黑色的,S的右孩子是紅色
在這種情況下我們在 N 的父親上做左旋轉,這樣 S 成為 N 的父親和 S 的右兒子的父親。我們接著交換 N 的父親和 S 的顏色,並使 S 的右兒子為黑色。子樹在它的根上的仍是同樣的顏色,所以屬性 3 沒有被違反。但是,N 現在增加了一個黑色祖先: 要麼 N 的父親變成黑色,要麼它是黑色而 S 被增加為一個黑色祖父。所以,通過 N 的路徑都增加了一個黑色節點。