遍歷組合算法的模塊化

在日常的需求設計中，遍歷組合是一個常見的問題。

　　例如：現在有N個不同的數。要求在其中找到M個數，使得M個數之和為指定的S，求所有滿足條件的組合。

　　這是一個很明顯的遍歷組合的問題。一般采用遞推算法，求出滿足條件的解。

　　這類問題一般都采用一個數組P，來存放解。遍歷整個組合空間，來找出解（有可能是所有解、也可能是一個解，根據題目要求來定）

　　由於這類問題解法是固定的，故在此把該算法模塊化。留待日後查閱用。

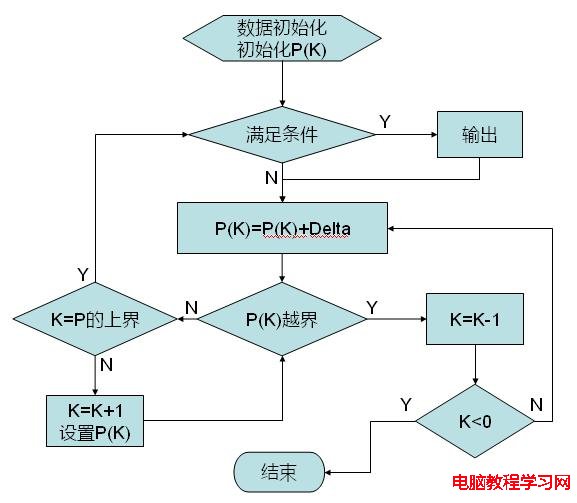
　　上圖是該算法的算法流程圖

　　下面貼出該算法的偽代碼，用的是VB2005

　　Public Sub Traversal()
　　　　Dim P() As Integer, K As Integer, IsGroup As Boolean

　　　　InitData()　　　　　　　　　　　　　　　　　　　　　　　　注：初始化數組代碼塊

　　　　K = P.GetUpperBound(0)

　　　　Do
　　　　　　If IsMatch() Then　　　　　　　　　　　　　　　　　　注：判別是否滿足條件的代碼塊
　　　　　　　　OutputAnswer() 　　　　　　　　　　　　　　　　注：輸出解的代碼塊
　　　　　　End If

　　　　　　IsGroup = False

　　　　　　Do
　　　　　　　　Delta(K)　　　　　　　　　　　　　　　　　　　　　注：P(K)自增加值的代碼塊
　　　　　　　　Do
　　　　　　　　　　If Overflow(K) Then　　　　　　　　　　　　　注：判斷P(K)是否越界的代碼塊
　　　　　　　　　　　　K = K - 1
　　　　　　　　　　　　Exit Do
　　　　　　　　　　Else
　　　　　　　　　　　　If K < P.GetUpperBound(0) Then
　　　　　　　　　　　　　　K = K + 1
　　　　　　　　　　　　　　SetP(K)　　　　　　　　　　　　　　　 注：依據條件設置P(K)值的代碼塊
　　　　　　　　　　　　Else
　　　　　　　　　　　　　　IsGroup = True
　　　　　　　　　　　　　　Exit Do
　　　　　　　　　　　　End If

　　　　　　　　　　End If
　　　　　　　　Loop
　　　　　　Loop Until (K < 0 Or IsGroup = True)

　　　　Loop Until K < 0

　　　　SomeEndCode()　　　　　　　　　　　　　　　　　　　　　 注：求解結束的代碼塊

　　End Sub

　　舉例說明：有1、4、7、2、5、6、9、8、7、5十個數，求四個數之和為20的所有組合。

　　分別闡述各個代碼塊的實現

　　初始化數組代碼塊：

　　　　Dim N() As Integer={1,4,7,2,5,6,9,8,7,5}

　　　　Redim P(3)

　　　　P(0)=0:P(1)=1:P(2)=2:P(3)=3

　　判別是否滿足條件的代碼塊：

　　　　N(P(0))+N(P(1))+N(P(2))+N(P(3))=20

　　輸出解的代碼塊：

　　　　Debug.Print N(P(0)) & "," & N(P(1)) & "," & N(P(2)) & "," & N(P(3))

　　P(K)自增加值的代碼塊：

　　　　P(K)=P(K)+1

　　判斷P(K)是否越界的代碼塊：

　　　　P(K)>K+6

　　依據條件設置P(K)值的代碼塊：

　　　　P(K)=P(K-1)+1

　　求解結束的代碼塊

　　　　本題沒必要設置這段代碼

　　故本題的代碼如下：

　　Public Sub Traversal()
　　　　Dim P() As Integer, K As Integer, IsGroup As Boolean

　　　　Dim N() As Integer={1,4,7,2,5,6,9,8,7,5}

　　把這類問題模塊化，以後碰到類似的問題。直接修改各個代碼塊的代碼。

　　著文以記之。