昨天我發過了平移的一篇文章,就有人說都有現存的算法存在了,不錯,我要提醒一下,我並不是什麼技術高超的學者,或者說是某某研究員,那麼我的算法怎麼來呢,有人說過天下文章一大抄,看你會抄不會抄,不知道大家有沒有去過那些論文網站,有沒有去那裡找過什麼論文,反正我是常去的,你去了你就會發現,他們的那些很多算法也是別人已經做過,已經寫過的。
我發在這裡也只是想起到一種提醒的作用,要說讓我自己想一個什麼高深的算法,我自認現在還沒有那個水平。
首先,在MDX中要通過鼠標的旋轉就知道,鼠標這時的移動並不是在一個平面內移動,而是在一個半球內移動的。
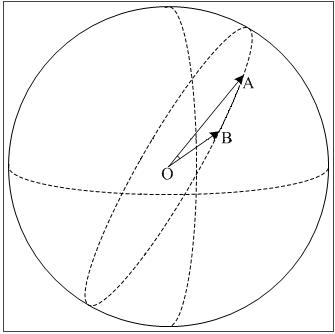
就象上圖中的從A到B點是按照圓的軌跡在移動,而不是按直線由A到B的。
旋轉之所有叫旋轉那就要有旋轉軸和旋轉角,旋轉軸也就是平面OAB的法向量,平面的法向量有公式可以求的,旋轉角一樣也有公式可以求:
n=OA×OB
α=ACOS((OA*OB)/(|OA|*|OB|))
在程序中旋轉角(α)可以設置為2倍,這樣如果用鼠標點擊視圖的左中邊緣,然後拖動至視圖的右中邊緣,則可實現模型以y 軸為旋轉軸的360旋轉,也就是一周。
現在的問題就成了求A,B兩點坐標的問題了,那麼這兩點的坐標怎麼樣的確定呢,注意有兩種情況:
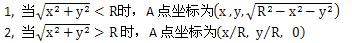
還 有一個問題就是R的大小,R一般會設置成為窗口寬度的一半;
到此要解決的問題除了一個問題也就差不多都解決了,那個問題下面再說,我將代碼copy到下面我在一句句說。。
1 float radius = (this.Width / 2) > (this.Height / 2) ? (this.Width / 2) : (this.Height / 2);
2 Vector3 preVector = new Vector3(); // 前一次鼠標與中心點的向量
3 preVector.X = _posLast.X - radius; //A點坐標
4 preVector.Y = _posLast.Y - radius;
5 float square = radius * radius - preVector.X * preVector.X - preVector.Y * preVector.Y;
6 if (square <= 0) //前面說到的兩tk
7 {
8 square = 0;
9 preVector.Z = 0;
10
11 preVector.X = preVector.X / preVector.Length();
12 preVector.Y = preVector.Y / preVector.Length();
13 }
14 else
15 {
16 preVector.Z = (float)Math.Sqrt(square);
17
18 preVector.X = preVector.X / radius; // 單位化
19 preVector.Y = preVector.Y / radius;
20 preVector.Z = preVector.Z / radius;
21 }
22
23 Vector3 curVector = new Vector3(); // 現在鼠標與中心點的向量
24 curVector.X = e.X - radius; //A點坐標
25 curVector.Y = e.Y - radius;
26 square = radius * radius - curVector.X * curVector.X - curVector.Y * curVector.Y;
27 if (square <= 0)
28 {
29 square = 0;
30 curVector.Z = 0;
31
32 curVector.X = preVector.X / curVector.Length();
33 curVector.Y = curVector.Y / curVector.Length();
34 }
35 else
36 {
37 curVector.Z = (float)Math.Sqrt(square);
38
39 curVector.X = curVector.X / radius;
40 curVector.Y = curVector.Y / radius;
41 curVector.Z = curVector.Z / radius;
42 }
43
44 if (preVector == curVector)
45 return;
46
47 Vector3 crossVector = Vector3.Cross(preVector, curVector);
48 float alpha = (float)Math.Acos(Vector3.Dot(preVector, curVector) / (preVector.Length() * curVector.Length()));
49
50 _matrixRotation.Multiply(Matrix.RotationAxis(crossVector, alpha * 2));
這裡我將最後的三句拿出來:
44-47:為什麼要有這兩句?這個可是為個算法裡面的一個比較關鍵的地方, 這個算法有一點小問題就是當OA與OB也就是preVector與curVector相隔非常小甚至相等的時候,大家想想會發生什麼事情,想想Vector3.Cross()這個函數是干什麼的,如果上面兩者相等會發生什麼,這個就是我在做的時候就找了好久才找到的這個缺陷 ,開始我還以為是算法本身有問題,就想了很多別的算法,繞了一大圈才找到這個。
48:求兩者之間的角度50:旋轉2倍的角度(個人習慣),這裡也要注意是每一次的旋轉都要累加到一起來,matrixRotation就起到了累加器的作用,並且還要是右乘上現在的旋轉量,不是左乘。
好了,現在這個也就說完了,其實也比較的簡單,其實技術就象我們老師說的一樣,技術就是一張紙,在捅破之前非常神秘,捅破之後就一錢不值了。