可伸縮性與加速比
可伸縮性是衡量應用程序加速比多少的尺度之一(注:加速比指應用程序串行化與並行化之間所花費時間之比,它表示並行化之後的效率提升結果)。2 倍的加速比表明並行程序僅需要花費串行程序的一半時間。比如理想情況下,運行在單處理器上的程序花費 30 秒,而在雙核機器上運行僅需花費 15 秒。
我們總是期望運行在雙核機器上的應用程序要比在單核上快的多。同理,運行在四核機器上也要比在雙核上快的多。這就好像以前當 CPU 換代升級時,隨著主頻提升,我們的程序總是可以運行的更快。很不幸,大多數應用程序在步入多核時代後,性能不但沒有提升,甚至有所降低。
假如我們增加更多的處理器核心數,而應用程序並沒有獲得額外的加速。從這點來看,該應用程序不具有可伸縮性。如果強制使用另外的處理器核心,通常會造成性能下降。因為這時分布式和同步的開銷開始凸顯威力。
更多關於可伸縮性的指導方針,樓主強烈推薦這篇文章:可伸縮性原則。
應用程序到底有多少並行性可言?
如小標題所說,應用程序到底有多少並行性呢?答案是視情況而定(廢話)。
顯然,這個問題取決於解決問題的多寡和發現並恰當利用並行算法的能力。我們先前大部分討論(更多討論請參見:並行思維 [I])都圍繞著如何在昂貴和稀有的並行計算機上編寫高性能程序。隨著多核處理器時代的到來,許多方面已經發生變化。我們需要退一步來重新審視一下。
Amdahl 定律
Gene Amdahl 發現在計算機體系架構設計過程中,某個部件的優化對整個架構的優化和改善是有上限的。這個發現後來成為知名的 Amdahl 定律。該定律告訴我們,假如我們以 2 倍加速程序的全部,那我們可以預期程序運行的比 2 倍更快。但是,假如我們只以 2 倍加速優化程序的一半,那麼整個系統只改善了 1.33 倍。Amdahl 定律很容易可視化表達。設想有個程序由 5 個相同的部分組成,且每個部分運行時間均花費 100 秒,如圖 1 所示:
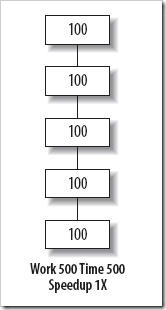
圖 1
如果我們以 2 倍和 4 倍來加速其中的兩部分,如圖 2 所示:
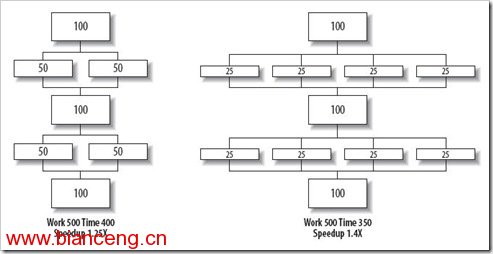
圖 2
那麼程序運行總時間將由原來的 500 秒分別縮減至 400 秒和 350 秒。 但是,我們也應該看到,更多的部分不能通過並行來加速。無論有多少處理器核心可用,串行部分 300 秒的障礙都不會被打破,如圖 3 所示:
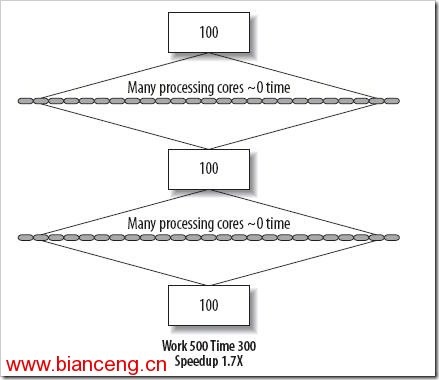
圖 3
上述最終表明,無論我們擁有多少處理器,都無法讓程序非並行(串行)部分運行的更快。
並行程序開發人員可以利用 Amdahl 定律來預測使用多少處理器來達到最大的加速比。Amdahl 定律是個悲觀定律,但業界還有另外一種視角來看待該問題,這就是接下來要講述的 Gustafson 定律(注:至於 Amdahl 及 Gustafson 定律的計算公式,大家可以 Google 之)。
Gustafson 定律
Sandia 國家實驗室的 John Gustafson 從一個不同的視角來重新審視 Amdahl 定律。他指出並行非常有用。因為隨著計算機越來越強大,應用程序會聚焦在更多工作上,而不是一個固定工作量。今天的應用程序幾乎都不運行在 10 年前的老機器上,甚至也很少運行在 5 年前的機器上。而且這並不局限在游戲領域,它同樣適用於辦公軟件,Web 浏覽器,圖形圖像處理軟件,以及像 Google Earth 此類的軟件。
其實,Amdahl 定律本身做了幾個假設,盡管這些假設在現實世界中不一定正確。第一個假設就是最優串行算法的性能嚴格受限於 CPU 資源的可用性。但是實際情況並非如此,多核處理器可能會為每個核實現一個單獨的 Cache,這樣,Cache 中就能夠存放更多的數據,從而降低了存儲延遲。Amdahl 定律的第二個缺陷就是它假定串行算法是給定問題的最優解決方案。但是,有一些問題本質上就是並行的,因此采用並行實現時所需的計算步驟就會比串行算法減少很多。
Amdahl 定律還有更大的缺陷,也就是第三點假設,關於問題規模的假設。Amdahl 定律假設在處理器核數量增長的時候,問題的規模保持不變。這在大多數情況下不成立。一般來講,當給予更多計算資源的時候,問題規模都會隨之增大以適應資源規模的擴大。對於很多問題來說,隨著問題規模增長時,需要解決的並行部分比非並行部分(即串行部分)增長的更快速。因此,隨著問題域增長,串行部分所占比例減少。參照 Amadahl 定律,程序可伸縮性得到增強。
仍然以 圖1 為例。假如問題隨著可用並行性伸縮,我們就能看到如圖 4 所示:
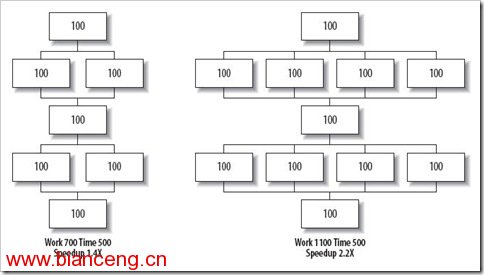
圖4
如果串行部分仍然花費相同的時間量,隨著其在整體中所占比例的下降,變得越來越不重要。最終的結果便如圖 5 所示,程序性能隨著處理器數量線性增長,復雜度為 O(n)。
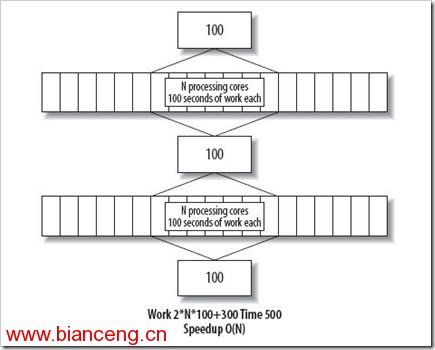
圖5
即便如此,程序的性能仍然非常受限於串行部分。投入了大量處理器只為那 40% 的效率提升。這在超級計算機上,無疑是恐怖的浪費。在多核處理器系統上,我們當然希望其他工作也能並發運行,以便能充分利用未能利用的處理能力。這是更加復雜的新世界。
無論我們采用 Amadahl 定律視角還是 Gustafson 定律視角,在任何情況下,最小化串行代碼都是良好的習慣。這兩大定律的觀點也都是正確的。不同之處在於你想要程序在既有工作量的前提下運行的更快,還是更快速的處理更大的工作量。不過實踐表明程序越復雜,要解決的問題規模越大。Gustafson 定律更加符合現實一點。盡管如此,Amadahl 定律仍然時刻困擾我們,如果你要在相同基准下,讓單一程序運行的更快。
通過切換到並行算法而不擴展問題規模,從而使得應用程序運行的更快。這通常比在更大的問題規模上使其運行更快困難的多。應用程序的可伸縮性可以歸納為並行化增長的工作量和最小化串行工作。Amadahl 定律促使我們努力減少串行部分,而 Gustafson 定律則告訴我們要考慮更大的問題域。尤其是相對串行工作來說, 並行化增長的工作量。
串行化算法 VS 並行化算法
有一個很明顯的事實是:最佳串行化算法很少是最佳並行化算法,反之亦然。這意味著要使程序在單核,多核系統上都運行良好,僅僅編寫良好的串行代碼或並行代碼並不夠。
超級計算機程序員從實踐中得知,並發任務工作量會隨著問題規模的功能快速增長。假如工作量的增長比串行化開銷(例如通信,同步)還要快,那麼僅通過問題規模的增長就可以判定程序可伸縮性不佳。程序不會說在 100 個處理器下可伸縮性不佳,而到了 300 個處理器下可伸縮性就變好了。
該如何應對多核的到來?很簡單,放棄過去的串行思維,開始並行思考。