如果有兩張分辨率為32x32的黑白圖片,要計算這兩張圖片的相似度該怎麼辦?
根據這篇文章《數學之美 系列 12 - 余弦定理和新聞的分類》的介紹,我們只需要計算一下兩個1024位(32x32=1024)的向量之間的夾角的余弦即可,結果越接近於1,相似度就越高。
好了,理論基礎有了,下面說怎麼存儲我們的向量。
因為圖片上只有兩種顏色,所以用1位二進制足以表示。那就認為白色的點為0,黑色的點為1。這樣,我們每一張圖片就可以放在32個32位整數裡,每行用一個整數表示,既節省了空間,又降低了操作時的復雜度。
接下來說如何計算。
如果老老實實的按照以下公式進行計算,我們需要取出整數中相應位的值,然後相乘或者分別平方,顯然這種方法很浪費時間。
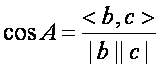
我們來看看有沒有什麼簡便方法。
因為我們只有0或者1兩種值,所以,分子中的相應位分別相乘,就可以轉化為相應位進行與運算,又因為我們使用了整型存儲,所以計算進一步簡化為兩個整數按位與。
而分母中的按位分別平方然後相加,就可以省掉平方的操作,直接按位相加了。
因此,整個程序的操作過程就可以按照如下步驟進行:
1.將每張圖片按像素存放到一個長度為32的32位整型數組裡面,每個整數存放一行,整數的每位存放一個像素值(0或者1);
2.計算分子時,將兩個這樣的數組中的整數按照對應的索引分別按位與,然後將計算結果按位相加;
3.計算分母時,將每個數組中的所有整數按位相加,然後開根號,最後相乘;
4.分子除以分母,得出余弦值。
第2、3、4步的代碼如下:
public double GetCosine(int[] e1, int[] e2)
{
int a = 0;//分母1
int b = 0;//分母2
int c = 0;//分子
for (int y = 0; y < 32; ++y)
{
//兩個數組中的整數按位與
int i = e2[y] & e1[y];
//按位加
for (int x = 1; x < 33; ++x)
{
c += (i >> x) & 1;
a += (e2[y] >> x) & 1;
b += (e1[y] >> x) & 1;
}
}
//計算分母
int d = a * b;
return d == 0 ? 0 : c / Math.Sqrt(d);
}
如果看到了這裡,你已經知道了我們該如何計算兩個圖片的相似度,按我的經驗,計算結果超過0.8,就可以認為這兩個圖片一樣了。
如果把這裡的圖片換成驗證碼,而你碰巧已經知道其中一個驗證碼的值,那麼另外一個驗證碼的值你現在也知道了。